6.5 Topology and Relationships Between Geometric Primitives

Topology is the subfield of mathematics that deals with the relationship between geometric entities, specifically with properties of objects that are preserved under continuous deformation. As will be illustrated in this section, the concepts of topology are very useful for geographers, surveyors, transportation specialists, and others interested in how places and locations relate to one another.

In the previous section, you learned how coordinates, both geometric and geographic, can define points and nodes, how nodes can build edges, and how edges create faces. We will now consider how nodes, edges, and faces can relate to one another through the concepts of containment, connectedness, and adjacency. A fundamental property of all topological relations is that they are constant under continuous deformation: re-projecting a map will not alter topology, nor will any amount of rubber-sheeting or other data transformations change relations from one form to another.

Containment is the property that defines one entity as being within another. For example, if an isolated node (representing a household) is located inside a face (representing a congressional district) in the MAF/TIGER database, you can count on it remaining inside that face no matter how you transform the data. Topology is vitally important to the Census Bureau, whose constitutional mandate is to accurately associate population counts and characteristics with political districts and other geographic areas.

Connectedness refers to the property of two or more entities being connected. Recall the visual representation of the geometric primitives in Figure 6.3. Topologically, node N14 is not connected to any other nodes. Nodes N9 and N21 are connected because they are joined by edges E10, E1, and E10. In other words, nodes can be considered connected if and only if they are reachable through a set of nodes that are also connected; if a node is a destination, we must have a path to reach it.

Connectedness is not immediately as intuitive as it may seem. A famous problem related to topology is the Königsberg bridge puzzle (Figure 6.5).

Try This: Can you solve the Königsberg bridge problem?

Figure 6.5: The seven bridges of Königsberg bridge puzzle.

Credit: Euler, L. "Solutio problematis ad geometriam situs pertinentis." Comment. Acad. Sci. U. Petrop. 8, 128-140, 1736. Reprinted in Opera Omnia Series Prima, Vol. 7. pp. 1-10, 1766.

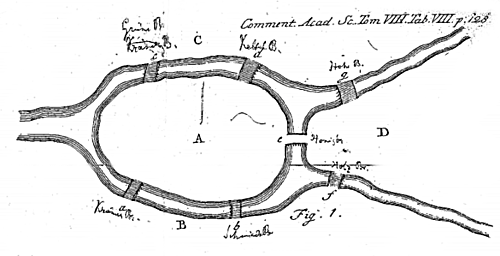
The challenge of the puzzle is to find a route that crosses all seven bridges, while respecting the following criteria:

1. Each bridge must be crossed;
2. A bridge is a directional edge and can only be crossed once (no backtracking);
3. Bridges must be fully crossed in one attempt (you cannot turn around halfway, and then do the same on the other side to consider it “crossed”).
4. Optional: You must start and end at the same location. (It has been said that this was a traditional requirement of the problem, though it turns out that it doesn’t actually matter – try it with and without this requirement to see if you can discover why.)

Take some time to see if you can figure out the solution. When you’ve found the answer or given up, scroll down the page to see the correct solution to the problem.

Did you find the route that crosses all seven bridges and meets the above criteria? If not, you got the right answer; there is no such route. Euler proved, in 1736, that there was no solution to this problem. In fact, his techniques paved the way for graph theory, an important area of mathematics and computer science that deals with graphs and connections. Graph theory is beyond the scope of this course, but it does have applications to geography. Interested readers can learn more about graph theory at Diestel Graph Theory.

The property of adjacency relates to entities being directly next to one another. In Figure 6.3, all of the faces are adjacent. This is easy to determine: if two faces share an edge, they are adjacent. Adjacency becomes less intuitive with other entities, however. See Figure 6.6 for an example of adjacency and why it cannot be simply assessed from a visual perspective:

Figure 6.6: Because nodes are zero-dimensional, they cannot be adjacent.

Credit: Joshua Stevens, Department of Geography, The Pennsylvania State University.

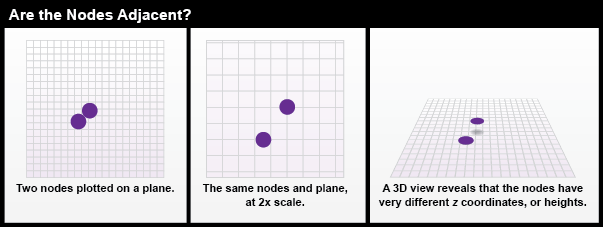
At first, the two nodes in Figure 6.6 might look like they are adjacent. Zooming in or tilting the plane of view reveals otherwise. This is because nodes, as points made from coordinate pairs, do not have a length or width; they are size-less and shapeless. Without any size or dimensionality, it is impossible for nodes to be adjacent. The only way for two nodes to ‘touch’ would be for them to have the exact same coordinates – which then means that there aren’t really two nodes, just one that has been duplicated.

This is exactly why features in the MAF/TIGER database are represented only once. As David Galdi (2005) explains in his white paper “Spatial Data Storage and Topology in the Redesigned MAF/TIGER System,” the “TI” in TIGER stands for “Topologically Integrated.” This means that the various features represented in the MAF/TIGER database—such as streets, waterways, boundaries, and landmarks (but not elevation!)—are not encoded on separate “layers.” Instead, features are made up of a small set of geometric primitives — including 0-dimensional nodes and vertices, 1-dimensional edges, and 2-dimensional faces —without redundancy. That means that where a waterway coincides with a boundary, for instance, MAF/TIGER represents them both with one set of edges, nodes and vertices. The attributes associated with the geometric primitives allow database operators to retrieve feature sets efficiently with simple spatial queries.

To accommodate this efficient design and eliminate the need for visual or mental exercises in order to determine topological states, the MAF/TIGER structure abides by very specific rules that define the relations of entities in the database (Galdi 2005):

1. Every edge must be bounded by two nodes (start and end nodes).
2. Every edge has a left and right face.
3. Every face has a closed boundary consisting of an alternating sequence of nodes and edges.
4. There is an alternating closed sequence of edges and faces around every node.
5. Edges do not intersect each other, except at nodes (note, this is a specialized use of the term "intersect" that includes the concept of "cross", which edges do not do, and "meet" which they can do).

Compliance with these topological rules is an aspect of data quality called logical consistency. In addition, the boundaries of geographic areas that are related hierarchically — such as blocks, block groups, tracts, and counties (all defined in Chapter 3) — are represented with common, non-redundant edges. Features that do not conform to the topological rules can be identified automatically, and corrected by the Census geographers who edit the database. Given that the MAF/TIGER database covers the entire U.S. and its territories, and includes many millions of primitives, the ability to identify errors in the database efficiently is crucial.

So how does topology help the Census Bureau assure the accuracy of population data needed for reapportionment and redistricting? To do so, the Bureau must aggregate counts and characteristics to various geographic areas, including blocks, tracts, and voting districts. This involves a process called “address matching” or “address geocoding” in which data collected by household is assigned a topologically-correct geographic location. The following pages explain how that works.