Note:
Analysis - Environments...should be set appropriately before doing any analysis (Figure 7.5).
In particular, use the centreCountyCivilDivisions layer as the Mask and also for the Processing Extent. You should also carefully consider what is an appropriate Cell Size for the analysis and set that parameter.
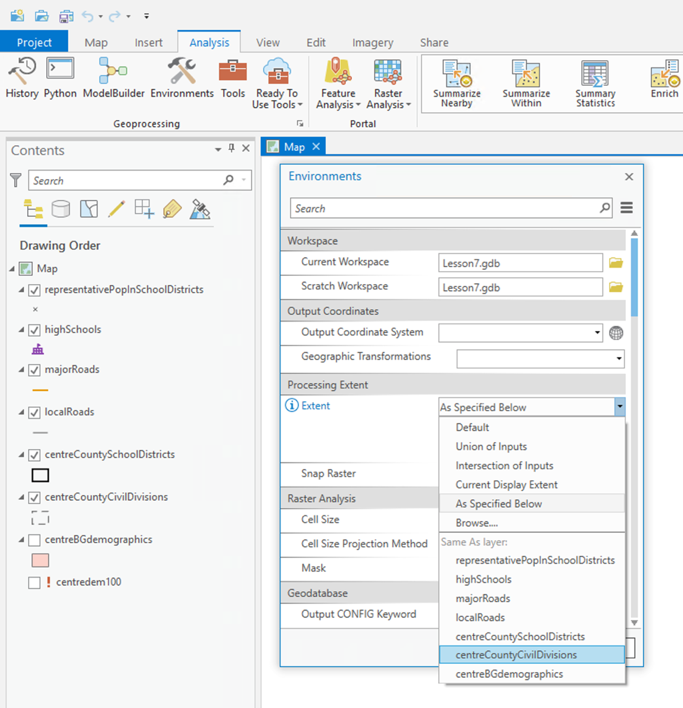
The first analysis we will do uses the Spatial Analyst Tools - Distance - Euclidean Allocation tool from the Tools menu (Figure 7.6). This allocates each part of the map to the closest one of a set of points and is the raster equivalent of proximity polygons.
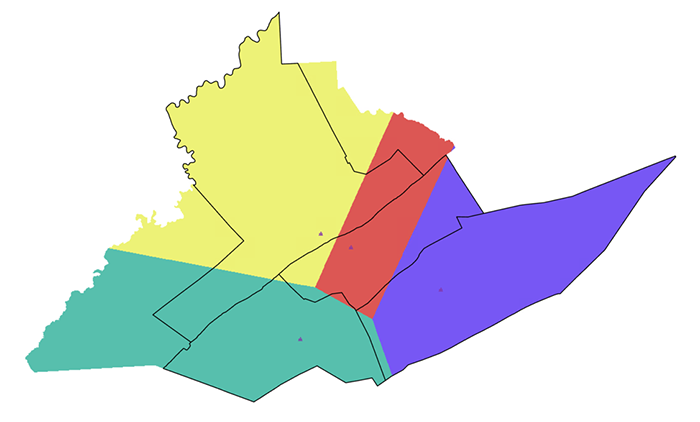
Running this Euclidean Allocation (straight line distance) analysis will produce an allocation layer (Figure 7.7).
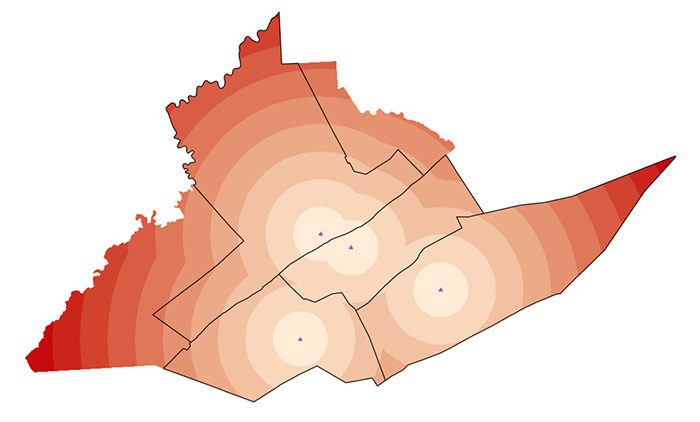
You can also request a distance layer (Figure 7.8).
You can further analyze these layers. For example, it may be easier to read the distance analysis if you create contour lines. The results of the allocation analysis can be converted to vector polygons, which might make subsequent analysis operations easier to perform, depending on which approach you decide to take.
Deliverable
In your Project 7 write-up, describe how the distance analysis operation works. In your description, comment on how you would combine multiple distance analysis results (one for each high school) to produce an allocation analysis output. [Hint: First run the Euclidean Distance Tool for each high school individually and then look for a tool that when used can generate the same map that the Euclidean Allocation analysis provides (i.e., the map shown in Figure 7.7). There is a tool which could help with this -- take a look at the tools available in Spatial Analyst - Local (e.g., Cell statistics or Lowest).]
As part of your discussion, include the output maps generated by the Euclidean Allocation and Euclidean Distance processes.
Finally, comment on the differences in the Euclidean (straight-line) distance allocation and the actual allocation of places to school districts. (You will need to look at the roads, topography, and minor civil divisions to make sense of this.)