4.4.2.2: Derivation of the Diffusivity Equation in Radial-Cylindrical Coordinates

The derivation of the diffusivity equation in radial-cylindrical coordinates will be the last topic in our discussion on individual well performance. It also gives us the opportunity to introduce the topic of material balance, as we will use this concept in the following derivation.

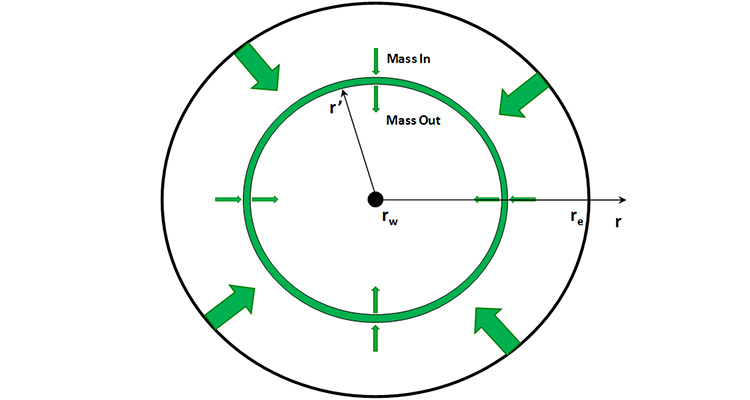
If we perform a mass balance on a thin ring or Representative Elemental Volume, REV, in the reservoir as shown in Figure 4.07, then we would have:

M a s s I n - M a s s O u t = M a s s A c c u m u l a t i o n

Equation 4.43

Equation 4.43 simply states that any mass entering the REV at its outer boundary less the mass exiting the REV at its inner boundary must be accumulating in the REV. We can elaborate on the definitions of terms in Equation 4.43 as:

M a s s I n = {ρ q]}_{r^{'} + d r} d t = 5.615 ({ρ q]}_{r^{'}} + \frac{\partial (ρ q)}{\partial r} d r) d t

Equation 4.44

M a s s O u t = 5.615 ({ρ q]}_{r^{'}}) d t

Equation 4.45

and,

M a s s A c c u m u l a t i o n = ϕ V_{b R E V} \partial ρ = 2 π r d r ϕ h \partial ρ

Equation 4.46

Where:

5.615 is a unit conversion constant, ft³/bbl
$ρ$ is the liquid density, lb/ft³
$q$ is the liquid rate, bbl/day
$r$ is the radial coordinate in a radial-cylindrical coordinate system, ft
$r'$ is the radius of the representative elemental volume, REV, ft
$q$ is time, days
$ϕ$ is the porosity of the reservoir, fraction
$V_{b}$ REV is the bulk volume of the representative elemental volume, REV, ft³
$h$ is the reservoir thickness, ft

Circular diagram showing mass in (equation 4.39) and Mass out (equation 4.40))

Figure 4.07: Representative Elemental Volume, REV, in Radial-Cylindrical Coordinates

Source: Greg King

Substituting Equation 4.44 through Equation 4.46 into Equation 4.43 results in:

5.615 [({ρ q]}_{r^{'}} = \frac{\partial (ρ q)}{\partial r} d r) - {ρ q]}_{r^{'}}] d t = 2 π r d r ϕ h \partial ρ

Equation 4.47a

or,

5.615 \frac{\partial (ρ q)}{\partial r} d r d t = 2 π r d r ϕ h \partial ρ

Equation 4.47b

Dividing by the term $5.615 r d_{r} d_{t}$ results in:

\frac{1}{r} \frac{\partial (ρ q)}{\partial r} = \frac{2 π ϕ h}{5.615} \frac{\partial ρ}{d t}

Equation 4.48

Now, substituting Darcy’s Law, Equation 4.05 with $l=-r$ and without the formation volume factor, B, (we want the flow rate in reservoir bbl/day not STB/day):

\frac{1}{r} \frac{\partial}{\partial r} [\frac{0.001127 ρ k (2 π r h)}{μ} \frac{\partial p}{\partial r}] = \frac{2 π ϕ h}{5.615} \frac{\partial ρ}{d t}

Equation 4.49

If we assume that the permeability, k, and the thickness, h, are uniform, then we have:

\frac{1}{r} \frac{\partial}{\partial r} (r ρ \frac{\partial p}{\partial r}) = \frac{ϕ μ}{(5.615) (0.001127) k} \frac{\partial ρ}{d t}

Equation 4.50a

or,

\frac{1}{r} \frac{\partial}{\partial r} (r ρ \frac{\partial p}{\partial r}) = \frac{ϕ μ}{0.006328 k} \frac{\partial ρ}{d t}

Equation 4.50b

or, after applying the chain rule:

\frac{1}{r} \frac{\partial}{\partial r} (r ρ \frac{\partial p}{\partial r}) = \frac{ϕ μ}{0.006328 k} \frac{\partial ρ}{d p} \frac{\partial p}{d t}

Equation 4.50c

Now, using the definition of compressibility for slightly compressible liquids:

c = \frac{1}{ρ} \frac{d ρ}{d p}

Equation 4.51

Substituting Equation 4.51 into results Equation 4.50c in:

\frac{1}{r} \frac{\partial}{\partial r} (r p \frac{\partial p}{\partial r}) = \frac{ϕ μ c ρ}{0.006328 k} \frac{\partial p}{d t}

Equation 4.52

Equation 4.52 is the nonlinear diffusivity equation. We say that it is Nonlinear because the two density terms in the equation are functions of pressure. In this nonlinear form, we cannot solve the equation analytically (exactly). In order to obtain analytical solutions to this equation, we must first Linearize it. To do this, we apply the chain rule to the left-hand side of Equation 4.52:

\frac{1}{r} [r (ρ \frac{\partial^{2} p}{\partial r^{2}} + \frac{\partial p}{\partial r} \frac{\partial ρ}{\partial r}) + ρ \frac{\partial p}{\partial r}] = \frac{ϕ μ c ρ}{0.006328 k} \frac{\partial p}{d t}

Equation 4.53a

or,

\frac{1}{r} {r [ρ \frac{\partial^{2} p}{\partial r^{2}} + {(\frac{\partial p}{\partial r})}^{2} \frac{\partial ρ}{\partial p}] + ρ \frac{\partial p}{\partial r}} = \frac{ϕ μ c ρ}{0.006328 k} \frac{\partial p}{d t}

Equation 4.53b

Note that the term, ${(\frac{\partial p}{\partial r})}^{2}$ , is the first derivative squared and not the second derivative, $\frac{\partial^{2} p}{\partial r^{2}}$ . To complete the linearization process, we must assume the pressure gradient, $\frac{\partial p}{\partial r}$ , is small. If this is the case, then ${(\frac{\partial p}{\partial r})}^{2}$ is very small, and we can remove it from Equation 4.53b:

\frac{ρ}{r} [r (\frac{\partial^{2} p}{\partial r^{2}}) + \frac{\partial p}{\partial r}] = \frac{ϕ μ c ρ}{0.006328 k} \frac{\partial p}{d t}

Equation 4.54a

or,

\frac{\partial^{2} p}{\partial r^{2}} + \frac{1}{r} \frac{\partial p}{\partial r} = \frac{ϕ μ c}{0.006328 k} \frac{\partial p}{d t}

Equation 4.54b

Which we can put into the compact format as:

\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial p}{\partial r}) = \frac{ϕ μ c}{0.006328 k} \frac{\partial p}{d t}

Equation 4.55a

or,

\frac{1}{r} \frac{\partial}{\partial r} (r \frac{\partial p}{\partial r}) = \frac{1}{η} \frac{\partial p}{d t}

Equation 4.55b

Where:

0.006328 is an equation constant (5.615 x 0.001127)
$r$ is the radial coordinate in a radial-cylindrical coordinate system, ft
$p$ is the pressure, psi
$ϕ$ is the porosity of the reservoir, fraction
$μ$ is the liquid viscosity, cp
$c$ is the liquid compressibility, 1/psi
$k$ is the reservoir permeability, md
$t$ is time, days
$η$ is the hydraulic diffusive $(η = \frac{0.006328 k}{ϕ μ c})$ , ft²/day

Equation 4.55 is the linear form of the diffusivity equation that describes the transient flow of a slightly compressible liquid through porous media. As we have already shown, solutions to this equation are useful in pressure transient analysis. The solutions to the diffusivity equation also have applications in the oil and gas production in:

Rate Transient Analysis (analysis of time-dependent production rates)
Type Curve Analysis (analysis of production rates using generalized, dimensionless plots)
Unsteady-State Aquifer Performance (performance of aquifers in contact with hydrocarbon reservoirs)

The name Diffusivity Equation comes from the fact that this equation governs the diffusion process (with appropriate changes to the equation parameters and variables to make it relevant for diffusion). In addition, this equation also governs the process of heat conduction in solids, again, with appropriate changes to the equation parameters and variables.

Navigation

EMS

Programs

Related Links