6.3.4.1: Multi-Phase Flow Correlations

As we have discussed, multi-phase flow through tubing is typically performed using empirical, multi-phase flow correlations. These empirical correlations are developed on the observations made by the investigator in laboratory experiments, field measurements, or both. The differences in the correlations are based on many factors including:

• experimental technique
  • tubing orientation
    • vertical
    • slanted
    • horizontal
  • tubing type
    • smooth
    • rough
  • fluids used in the experiments
    • air-water
    • crude oil - natural gas
  • pressure-temperature range used in the experiments
• flow regimes observed during the experiments and how they are incorporated into the correlations
• trade-off between the desired accuracy and the desired degree of mathematical simplicity or ease of application

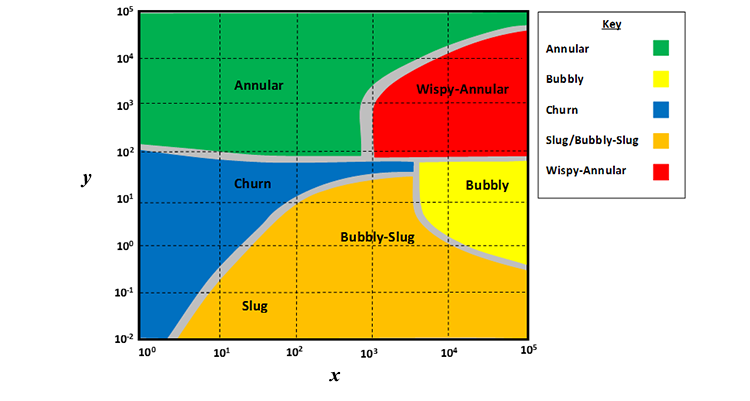
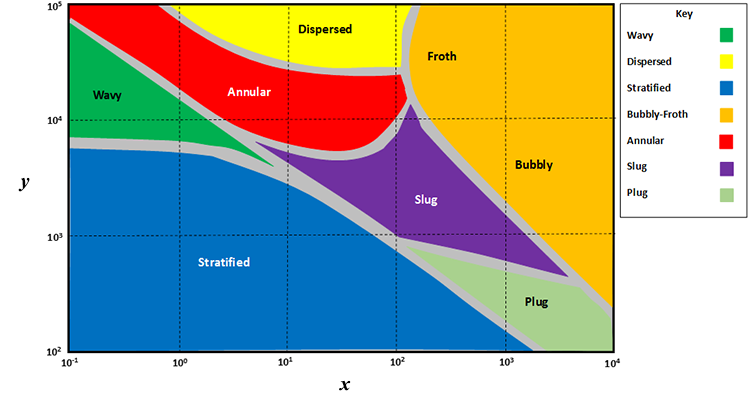
In most cases, the multi-phase flow correlations are based on the flow regimes that we have already discussed. For use in a multi-phase flow correlation, these flow regimes are plotted as Flow Pattern Maps. Examples of the flow pattern maps are shown in Figure 6.11 (for vertical flow) and Figure 6.12 (for horizontal flow).

Figure 6.11: Hewitt and Roberts Flow Regime Map for Vertical Flow (Redrawn)
Where: $x={\rho }_l{v}_l^2\left(\frac{l{b}_m}{ft-{\sec }^2}\right)$ and $y={\rho }_g{v}_g^2\left(\frac{l{b}_m}{ft-{\sec }^2}\right)$

Source: Greg King © Penn State, licensed CC BY-NC-SA 4.0

Figure 6.12: Original Baker Flow Regime Map for Horizontal Flow (Redrawn)
Where: $x=\frac{{\rho }_l{v}_l}{{\rho }_g{v}_g}{\left(\frac{{\rho }_g{\rho }_l}{{\rho }_{air}{\rho }_w}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left\{\frac{{\sigma }_w}{{\sigma }_l}{\left[\frac{{\mu }_l}{{\mu }_w}{\left(\frac{{\rho }_w}{{\rho }_l}\right)}^2\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$3$}\right.}\right\}\left(Dimensionless\right)$
and $y=3,600{\rho }_g{v}_g{\left(\frac{{\rho }_g{\rho }_l}{{\rho }_{air}{\rho }_w}\right)}^{-\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\left(\frac{l{b}_m}{f{t}^2\sec }\right)$

Source: Greg King © Penn State, licensed CC BY-NC-SA 4.0

The example flow regime maps shown in Figure 6.11 and Figure 6.12 illustrate two important points. The first point is how the flow regimes are incorporated into the flow correlations. The variables on the x-axis and y-axis are calculated, and that point on the map indicates the flow regime that is occurring in a well segment based on the investigator’s experimental or field results. For the flow regime identified on the flow pattern map, different mathematical expressions are used to quantify the Liquid Hold-Up, Gas Hold-Up, the slip velocity, and the friction factors within that particular flow regime. These dynamic data are the data that I identified in Table 6.05 with the blue cells. Once the dynamic data are calculated for a particular segment in a segmented well model, they are used in the energy balance equation to determine the pressure loss in that segment.

The second point illustrated by the example flow pattern maps is that the definitions of the x-axis and y-axis are different for each multi-phase flow correlation. This gets back to the empirical nature of the multi-phase flow correlations. Different investigators and different experimental/field procedures may result in different mathematical groups controlling the dynamics of the flow. The choice of these mathematical groups may also lie in the personal preference of the investigator.

For multi-phase flow, the fluid properties are typically calculated as mixture properties. These mixture properties are based on the Phase Hold-Up, $H_l$ and $H_g$. Hold-Up is the local fraction of the pipe volume occupied by the phase. In multi-phase flow correlations, the hold-up is determined from the map based on the mathematical expressions related to the flow regime. Once the hold-up is determined, fluid properties can be determined for the flowing mixture by:

for viscosity, some investigators prefer to use a different definition of mixture viscosity:

As a practical point, a working production engineer typically is not expected to know the details of the multi-phase flow correlation used in a well model. There is no universal rule for selecting the proper correlation for use for a particular well, group of wells, or wells in a field. The production engineer simply performs Flow Tests on his/her wells to see the actual pressure drops at the current reservoir conditions (orange and yellow table entries in Table 6.05) for known production rates and selects the multi-phase flow correlation that best matches the flow test results. Many software packages allow for the use of different multi-phase flow correlations for different segments of a segmented well model for one well. In other words, one well may use a different multi-phase flow correlation along different segments of the well.

Description of Multi-Phase Flow Correlations in Use in the Oil and Gas Industry

There are many multi-phase correlations used in the oil and gas industry. It is beyond the scope of this course to discuss all of the correlations in use today. Table 6.06 lists many of these correlations used in industry software along with notes describing their preferred applications.