2.6 Let's Convert Solar Time to an Angle

Reading Assignment

SECS, Chapter 6: Review both sections of "Moments, Hours, and Days" as well as Sun-Observer Angles."

In reviewing these sections, you should notice that three common angular symbols keep popping up: the declination ( $δ$ ), the local latitude ( $ϕ$ ), and the hour angle ( $ω$ ). As we shall again see in the next section, these are three of our key Earth-Sun angles.

We additionally include the use of longitude ( $λ$ ) in our calculation of time, and in particular, converting time to an angle: the hour angle.

Now, let's convert "time" into an angle, for our future trigonometric relations:

When we convert time to an angular value, we can no longer use a 24 hr format. We need to convert hourly time into a useful angle based on the properties of a sphere, again using spherical trigonometry.

Video: Hour Angles (5:03)

Hour Angles

Click Here for Transcript of Hour Angles Video

So, I'm sure a lot of you are wondering what we do with the hour angle. Because it's not something that we really ever used before in regular everyday language. But because so many of our mathematical calculations are in terms of angles, remember, angles are coordinates in the solar reference in the solar frame of reference.

So, when we normally have 24-hour time, we need to convert that time into something on the order of 360 degrees or, in our case, minus 180 degrees to plus 180 degrees. And so, we're going to figure out a way to convert 24 hours of time to degrees. And those degrees are going to be found as the hour angle.

So, time is going to be in terms of decimal hours. So time in decimal hours. And we're going to make sure that we do that in a 24-hour time frame, so that if I were talking about 1:30 in the morning, I would represent this as 1.5. If I wanted 1:30 in the afternoon, based on the 24-hour system, that would be 13.5. So we have that understood.

So, in order to get the hour angle of time, we're going to start with time is going to be the hour angle times the conversion of one hour per 15 degrees of rotation of the earth. So that's going to give me my decimal hours-- multiplying right there-- such that if I wanted to have the hour angle, I would have time times 15 degrees per one hour. In which case, my time is in hours. The units of hours would cancel out. And I'd be left with units of degrees.

Now, one of the things that you're going to find in your problems is the calculation of day length. And if the day length in the textbook is shown by calculating the hour angle of the sunset-- and we do sunset because it's a positive angular value. Basically, if I were to-- here, let me do a quick diagram.

If I were to put noon, 12:00 noon here, any time before noon would be negative. Any time after noon would be positive. So, this is where I have my negative 180 degrees going into the morning. You're looking back before noon, so you have negative degrees. Going into the afternoon, you're going after 12. So, you're adding degrees. So it's positive.

So, I have a positive value for the sunset. So, if I wanted to calculate the sunset, we find that I need to calculate the arc cosine or the inverse cosine of the negative tangent of the declination times the tangent of the latitude, phi. And I might have switched these two guys around in the textbook. But you're going to get the same answer.

So, that will give me the time of sunset or the hour angle of sunset. And the hour angle of sunrise is going to be the negative of the sunset. And then the last part that you're looking for, hours in a day, is going to be 2 times the sunset hour angle times the conversion of one hour for 15 degrees. That's going to give you the number of hours in the day. And you're going to want that for one of your answers as well.

Credit: Jeffrey R. S. Brownson © Penn State University is licensed under CC BY-NC-SA 4.0

Finishing Step for Time Conversions! The Hour Angle ( $ω$ ) in decimal degrees.

We represent the apparent displacement of the sun away from solar noon, either as a negative or positive angle. An $ω$ of zero indicates that the sun is at its highest point for that given day.

The sign of the hour angle before noon is negative, because we have to count backward from the "zero hour" of solar noon.
The sign of the hour angle after noon is positive, because we are counting forward from the "zero hour" of solar noon.

Another way of looking at it is the angular difference between the local meridian of the observer/collector and the meridian that the beam of the sun is intersecting at a given moment.

$ω = \frac{360^{\circ}}{24 hr} (t_{s o l} - 12) = \frac{15^{\circ}}{hr} (t_{s o l} - 12)$ $ω = {\begin{matrix} - 0 - 180 degrees, if before noon (morning) \\ + 0 - 180 degrees, if after noon (evening) \end{matrix}$

Now, the day won't really begin at -180 degrees, anywhere between the arctic circles. However, I wanted to emphasize that the day only begins at -90° on two days a year. Those days occur during the Equinox moments in the orbit of the Earth about the Sun, and the length of those days is actually 12 hours long. All other days are either shorter than 12 hours, or longer than 12 hours. As such, they end either less than 90° or greater than 90°.

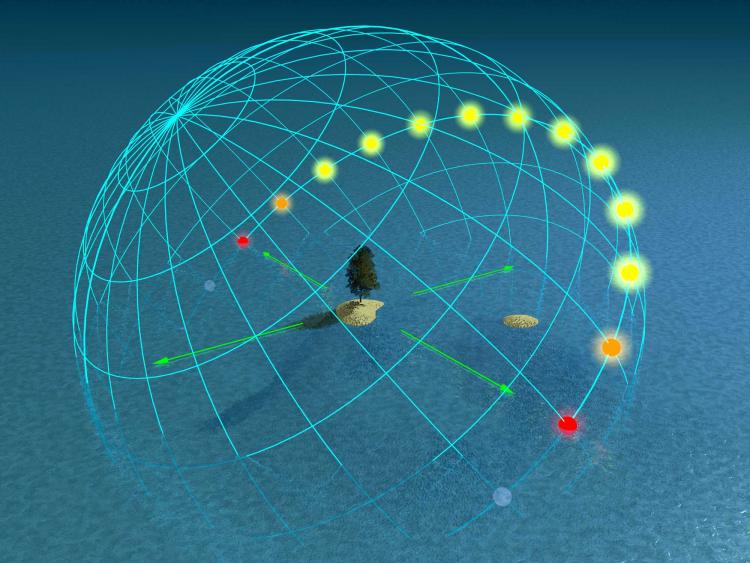
Sun Path on graphed sphere with a tree in the middle. Sun follows equator. More in caption below .

Figure 2.9: The Sun Path projected onto graphed sphere for a latitude of 50 degrees, and the day of an Equinox (12 hours). The hours for 8h00, 12h00, and 14h00 are listed in solar time, along with the associated hour angles of -60°, 0°, and +30°.

Credit: Original by Tau'olunga from Wikimedia Commons licensed under CC BY-SA 2.5 - Modified by J. Brownson.

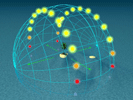
The images below demonstrate singular arcs of the Sun for each hour in solar time, at five different latitudes on Earth (no analemma correction necessary). The peak hour (or the hour with the highest solar altitude angle) is defined as solar noon. You will notice that the solar equinox has twelve sun spots for latitudes below the arctic circle, and that the sun rises due East, while setting due West. During the solar solstices, you see multiple arcs: one for winter and one for summer. Notice that there are more hours of the day in the summer, and the sun rises farther from the equator in the Summer (sun rise in the northeast for the Northern Hemisphere).

What else do you notice in comparing the four critical times of year at different latitudes?