2.12 Siting using Sun Paths and Spherical Coordinates

In a spherical coordinate system, the angles are the coordinates. So, if I were standing in a field in North Dakota, looking at something tall like an enormous wind turbine, I could define the position of the top of the nacelle relative to me by stating the general azimuth angle ($\gamma$, the rotation across the horizon from due South) and the general altitude angle ($\alpha$, the rotation up from the horizon). Effectively, this is my x ($\gamma$) and y ($\alpha$) coordinates on an orthographic projection of the sky dome on a flat surface.

Figure 2.15: A common example of spherical coordinates (r, $\theta$, $\varphi$) commonly used in physics: radial distance r, polar angle $\theta$ (theta), and azimuthal angle $\varphi$ (phi). The symbol $\rho$ (rho) is often used instead of r.

Credit: 3D Spherical Coordinates by Andeggs from Wikimedia (Public Domain)

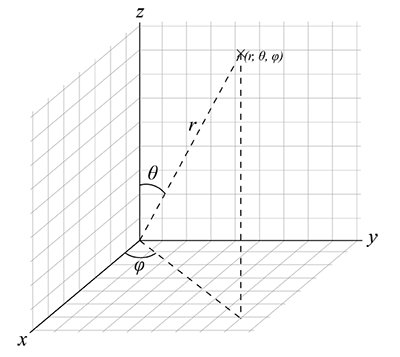
Many of you will be familiar with Cartesian coordinates in space (x, y, z). However, when dealing with spatial relations of spherical objects like the Earth and the Celestial Sphere, we find that working with basic spherical coordinate systems makes trigonometry available to us to solve for space and time equations. For spherical coordinates, we need information of radial distance, zenith angle, and azimuth. However, in solar positioning studies, a radius of one (unit radius) is all we need to establish a unit vector, and we are left with equations for only the zenith angle and azimuth (and the complement of the zenith angle, the altitude angle). Note how the zenith angle in Figure 2.15, above (the generic $\theta$ angle), is congruent with the solar zenith (${\theta }_z$) of the Sun, and the generic azimuth angle ($\phi$) is congruent with the solar azimuth (${\gamma }_s$).

The following equations describe the Cartesian coordinates (x, y, z) for unit vectors, followed by the equivalent functionals using the complementary altitude angle.
$$\begin{array}{c}\begin{array}{ccccc}z& =& \cos \theta & =& \sin \alpha \\ x& =& \sin \theta \cos \phi & =& \cos \alpha \cos \phi \\ y& =& \sin \theta \sin \phi & =& \cos \alpha \sin \phi \end{array}\end{array}$$

As seen in Figure 2.16, we need to pull back to our old trigonometry mnemonics! Recall "Soh Cah Toa" when looking at the figure:

Figure 2.16: Right Triangle with side lengths [a (opposite), b (adjacent), h (hypotenuse)] and angles [A, B, C].

Credit: J. Brownson © Penn State University is licensed under CC BY-NC-SA 4.0

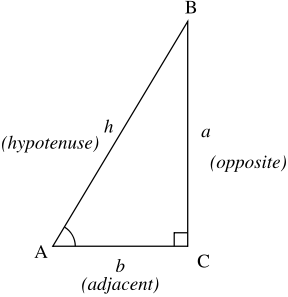
• Sine(A): Opposite over Hypotenuse (a/h)
• Cosine(A): Adjacent over Hypotenuse (b/h)
• Tangent(A): Opposite over Adjacent (a/b)