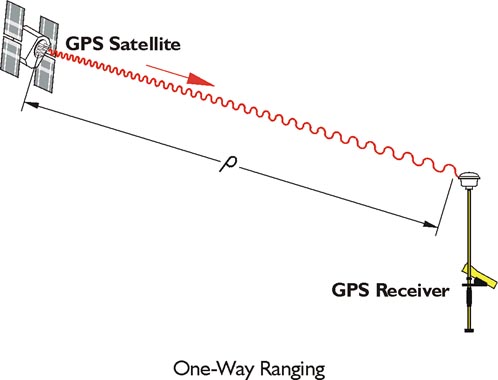
The one-way ranging used in GPS is more complicated. The broadcast signals from the satellites are collected by the receiver, not reflected. Nevertheless, the same measurement concept is used. In general terms, the full time elapsed between the instant a GPS signal leaves a satellite and arrives at a receiver, multiplied by the speed of light, is the distance between them. Unlike the wave generated by an EDM, a GPS signal cannot be analyzed at its point of origin. The measurement of the elapsed time between the signal’s transmission by the satellite and its arrival at the receiver requires two clocks (aka oscillators), one in the satellite and one in the receiver. This complication is compounded because these two clocks would need to be perfectly synchronized with one another to calculate the elapsed time, and hence the distance, between them exactly. Since such perfect synchronization is impossible, the problem is addressed mathematically.
In the image, the basis of the calculation of a range measured from a GPS receiver to the satellite, ρ, is the multiplication of the time elapsed between a signal’s transmission and reception, Δt, by the speed of light, c. A discrepancy of 1 microsecond, 1 millionth of a second, from perfect synchronization, between the clock aboard the GPS satellite and the clock in the receiver can create a range error of 299.79 meters, far beyond the acceptable limits for nearly all surveying work.
So, since perfect synchronization is not in the cards, we have to solve for time.