Both EDM and GPS ranging use the method represented in this illustration. In GPS, the measurement of the difference in the phase of the incoming signal and the phase of the internal oscillator in the receiver reveals the small distance at the end of a range.
By comparing the phase of the signal returned from the reflector with the reference wave it kept at home, an EDM can measure how much the two are out of phase with one another. However, this measurement can only be used to calculate a small part of the overall distance. It only discloses the length of a fractional part of a wavelength used. This leaves a big unknown, namely the number of full wavelengths of the EDM’s modulated carrier between the transmitter and the receiver at the instant of the measurement. This cycle ambiguity is symbolized by N. Fortunately, the cycle ambiguity can be solved in the EDM measurement process. The key is using carriers with progressively longer wavelengths. For example, the submeter portion of the overall distance can be resolved using a carrier with the wavelength of a meter. This can be followed by a carrier with a wavelength of 10 meters, which provides the basis for resolving the meter aspect of a measured distance. This procedure may be followed by the resolution of the tens of meters using a wavelength of 100 meters. The hundreds of meters can then be resolved with a wavelength of 1000 meters, and so on.
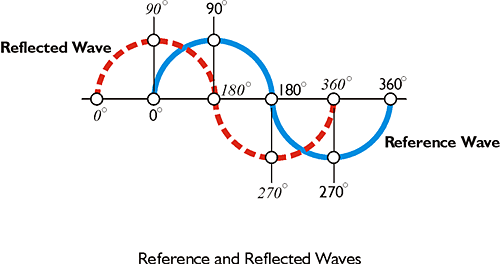
Here is that comparison, the reference wave in blue with the reflected wave with the dashed red line. The reflected wave came back out of phase by a quarter of a wavelength. With an EDM, wavelengths of varying length can be sent out. For example, if the EDM sends out a wavelength of 100 meters, then by looking at the fractional part of that 100-meter wavelength, it would be possible to determine the tens of meters in the distance. The hundreds of meters of the overall distance could be resolved by sending out a wavelength of 1,000 meters and looking at the fractional part (by phase comparison). This method depends on the fact that the EDM survey can send out waves of different wavelengths and have them return to where they came from. That makes comparison of the returned wave with the reference wave possible. By comparing phase angles, the fractional part of the wavelength that went out can be determined. The components of the total distance are built up by sending on wavelengths of different size; first the thousands of feet, then the hundreds of feet, then the single feet, and finally the decimals of feet. However, this whole method is not possible in GPS surveying. There are only three carriers; L1, L2, and L5. They have constant wavelengths. Therefore, while it's possible to determine the fractional part of the wavelength, that one small component of the distance, from a single measurement, knowing the number of full wavelengths between the receiver and satellite is more difficult. This is known as the integer ambiguity problem.