Imperfect Oscillators and Clock Corrections

Enter Time Differences

Source: GPS for Land Surveyors

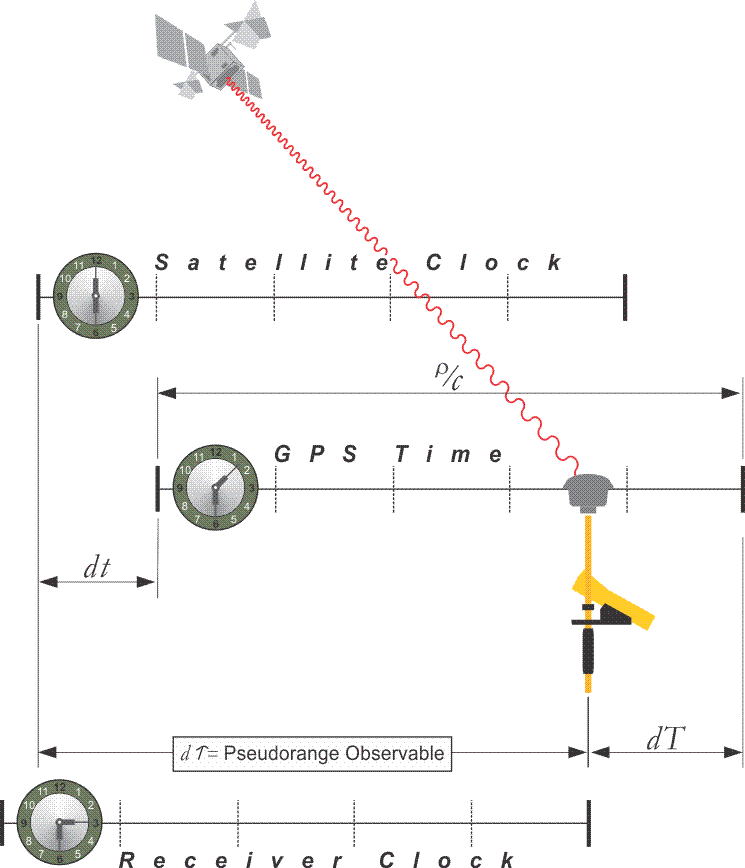
One reason the time shift, dτ (d tau), found in autocorrelation cannot quite reveal the true range, ρ, of the satellite at a particular instant is the lack of perfect synchronization between the clock in the satellite and the clock in the receiver. Recall that the two compared codes are generated directly from the fundamental rate, F_o, of those clocks. And since these widely separated clocks, one on Earth and one in space, cannot be in perfect lockstep with one another, the codes they generate cannot be in perfect sync either. Therefore, a part of the observed time shift, dτ (d tau), must always include the disagreement between these two clocks. In other words, the time shift not only contains the signal’s transit time from the satellite to the receiver, it contains clock errors, and other errors too. In fact, whenever satellite clocks and receiver clocks are checked against the carefully controlled GPS time, they are found to be drifting a bit. Their oscillators are imperfect. It is not surprising that they are not quite as stable as the atomic clocks around the world that are used to define the rate of GPS time. They are subject to the destabilizing effects of temperature, acceleration, radiation, and other inconsistencies. In other words, clock offsets bias every satellite to receiver pseudorange observable. The difference between the satellite clock's time and GPS time is shown in dt (d small t) in the illustration. The difference in the receiver's clock from GPS time is shown in dT (d capital T) in the illustration. While the pseudorange observable shown here in dτ (d tau) is intended to be the amount of time that it took the signal to reach the receiver from the satellite, there are some difficulties. Among them are the fact that the receiver's clock is probably a quartz oscillator, and it's not terribly stable, and the clock correction in the Navigation Message which was uploaded some time before it is received isn't exactly right either. Such discrepancies are important when a nanosecond, a billionth of a second, is approximately a foot. Therefore, the pseudorange has some errors that are difficult to remove. The pseudorange, by itself, while it has the virtue of being approximately correct, is certainly not at the level of accuracy that we have come to expect from GPS.  That is one reason it is called a pseudorange (i.e. false range)