We can increase the complexity of the zero-dimensional model by incorporating the atmospheric greenhouse effect in a slightly more realistic manner than is embodied by the ad hoc gray body model explored in the previous lecture. We now include an explicit atmospheric layer in the model, which has the ability to absorb and emit infrared radiation.
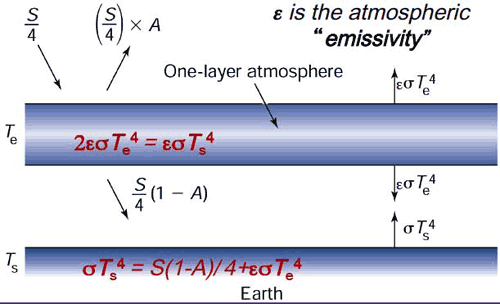
We will approximate the emissivity of Earth's surface as one, that is, we will assume that The Earth's surface emits radiation as a black body. The atmosphere itself has a lower but non-zero emissivity, i.e., it emits a fraction of what a black body would emit at a given temperature. This emissivity is due to property of greenhouse gases within the atmosphere, and we will denote this atmospheric emissivity by (not to be confused with the epsilon of previous lessons which was associated with the emissivity of Earth's surface, which we are approximating here as unity!). According to Kirchhoff's Law, at thermal equilibrium, the emissivity of a body equals its absorptivity (i.e., the fraction of incident radiation that is absorbed by the body). Therefore, is also a measure of the efficiency of the atmosphere's absorption of any infrared radiation (IR) incident upon it. IR radiation that is not absorbed by the atmosphere is transmitted through it; therefore, is the fraction of incident IR radiation that is transmitted through the atmosphere without being absorbed.
An of zero corresponds to no greenhouse effect at all, while an of unity corresponds to a perfect IR absorber, i.e., a perfect greenhouse effect. The true greenhouse effect is, of course, somewhere in between, i.e.,
We denote the effective albedo of the Earth system (i.e., the portion of incoming solar radiation immediately reflected back to space) as A, and we will now distinguish between the atmospheric temperature (which we will envision as representing the mid-troposphere, somewhere around 5.5 km above the surface where roughly half the atmosphere by mass lies below) and the surface temperature TS.
is related to, but not equivalent to, another quantity known as the effective radiating temperature, which we will denote as . is the temperature the Earth would have if it were a black body, i.e., if there were no greenhouse effect. It can be thought of as the temperature at the effective height in the atmosphere from which Earth is radiating infrared radiation back to space. In the limit of a perfectly emissive atmosphere ( ), as you can verify from our mathematical treatment below, we would have the equality = .
You may recall from our earlier discussion (in Lesson 1) of the vertical structure of the atmosphere, that atmospheric temperatures cool on average roughly in the troposphere — what is known as the standard lapse rate.
For the approximate current value of the solar constant S = 1370 W / m2, we saw in Lesson 4 that the black body temperature, i.e., the effective radiating temperature , is roughly 255 K.
Think About It!
Given that the Earth's average surface temperature is = 288 K, the effective radiating temperature is = 255 K, and the standard lapse rate is , can you determine the effective radiating level in the atmosphere?
Click for answer.
This is at the level of the mid-troposphere.
We can now express the condition of energy balance at each level in our simplified model of the Earth:
- The top of the atmosphere
- The atmospheric layer, which we can think of as centered in the mid-troposphere
- The surface
Balancing incoming and outgoing radiation at the top of the atmosphere gives:
Balancing incoming and outgoing radiation from the atmospheric layer gives :
- (Note that short wave radiation is not included in this balance because the atmosphere does not absorb in short wave range.)
Finally, balancing incoming and outgoing radiation at the surface gives:
Solving the system of equations for and gives:
Or more simply
Let us use the standard values of A = 0.3 and S = 1370 W / m2.
- If we take = 0 (which is equivalent to there being no greenhouse effect), we get our original blackbody result = 255 K = -18°C. Too cold!
- If we take = 1 (which is equivalent to a perfectly IR absorbing atmosphere), we get the result = 303 K = 30°C. Too warm!
- However, if we take = 0.77 (i.e., the atmosphere absorbs 77% of the IR radiation incident upon it), we get a result, = 288 K = 15°C. Just right!
Using (7) and = 288 K, we also get the result = 242 K. This is modestly lower than the effective radiating temperature = 255 K, indicating that it is found at about 5.5 km — a modestly higher level in the atmosphere than 5.1 km that you calculated earlier.
Of course, this model is still rather simplistic. For one thing, it only takes into account short wave and long wave radiation. We haven't accounted for important processes involved in the energy budget of the actual atmosphere and surface, which includes convection, latent heating, and the effect of large-scale motion.
We can nonetheless add some further realism to the model by incorporating some of the feedbacks we have discussed previously. In Problem Set 4 you will investigate a slightly more sophisticated version of the standard one-layer model. The model allows for the contribution of clouds to both the Earth's albedo and the longwave absorptive properties of the atmosphere in a very rough way. It also accounts for the positive ice albedo and water vapor feedbacks in a very rough manner.
Each of the feedbacks in the model will be expressed in the form of a feedback factor that you can vary. A feedback factor measures the relative magnitude of a feedback in terms of the amplitude of the response relative to the original forcing. If the response is equal in magnitude to the original forcing, there is no feedback, and the feedback factor is zero. If the response is double that of the original forcing, the feedback factor is one. For example, if a warming of 1°C due to doubling alone causes an increase in water vapor content that adds an additional equilibrium warming of 2°C, so that the net warming is 3°C, the water vapor feedback factor would be two. Feedback factors can be specified for a particular feedback (e.g., the water vapor feedback), or for the sum over all feedbacks under consideration (e.g., water vapor feedback, ice albedo feedback, and cloud feedback). For example, suppose that the initial 1°C warming, which led to 2°C warming due to water vapor feedback, also led to an increase primarily in low cloud cover, which added a relative cooling of -0.5°C, and a melting of ice, which added an additional relative warming of 1°C. Then the cloud feedback factor would be -0.5, the ice albedo feedback factor would be 1.0, and the net feedback factor would be 2 - 0.5 + 1 = 2.5! Alternatively, we could compute the overall feedback factor by taking the total warming (initial 1°C warming + 2°C - 0.5°C + 1°C = 3.5°C) divided by the initial warming, minus one, i.e., (3.5°C/1°C) - 1 = 2.5. The equilibrium climate sensitivity in this case would be 3.5.
While we have measured the feedback factors in terms of the temperature responses, one could also compute these factors in terms of the associated radiative forcing. For example, we know from earlier in the course that the radiative forcing due to doubling is roughly 3.7W/m2. Suppose that the increased greenhouse forcing associated with the water vapor feedback led to an additional downward long wave radiative flux of 7.4 W/m2 (and let us assume for this example that the other feedbacks are zero). Then the water vapor feedback factor would be 7.4/3.7 which is, again, two. The total downward radiative forcing would be 3.7W/m2 +7.4W/m2 =11.1 W/m2 total downward and the overall feedback factor would be 11.1/3.7 - 1 = 2!
Video: One Layer Energy Balance Model (3:56)
PRESENTER: Here is our One Layer Energy Balance Model. Right now it's set for the default settings of the various feedback factors.
The cloud feedback factor is set at a modestly negative value of minus 0.83. The water vapor feedback factor is 2. And the ice albedo feedback factor is 0.5. So these two, the water vapor feedback and the ice albedo feedback, are set at positive values. The cloud ready to feedback is set at a negative value.
And these values are roughly equal to the best current estimates of what those feedback factors are. And so using those default settings gives us sort of a mid-range climate sensitivity. And you'll look at that in your problem set.
So you can calculate the climate sensitivity of course by varying the CO2. And the CO2 can be varied with this lever here. Pre-industrial levels, 280 parts per million. Obviously 560 PPM is twice pre-industrial. If you like, you can even set values outside these ranges by going to the box down below. For example, I could set the CO2 level at 700 PPM.
And we can see the initial temperature-- surface temperature-- to 88k for the standard default settings. The new surface temperature, 292, that was a 4.1 degree warming of the surface. The atmosphere itself-- the mid troposphere-- warmed somewhat less, 3.4k.
We can see what the longwave and the shortwave forcings are. So these are estimates of the radiative forcing due to the combination of the direct influence of changing the CO2 levels, plus the various feedbacks-- the water vapor feedback, increasing the greenhouse gas concentration, giving us longwave forcing, that adds to the longwave forcing from the increase in CO2 alone.
The ice albedo feedback playing into the shortwave forcing. The cloud radiative feedback can influence both a combination of shortwave and long wave forcing. There's the cloud albedo effect, which tends to be a negative feedback. But there's also the greenhouse gas-like properties of clouds, the infrared absorbing properties of clouds which gives us a positive feedback. And as we vary this feedback factor, we can transition from where the negative cloud radiative feedbacks dominate to where the positive cloud feedback dominate.
We can see how the albedo changes as we vary the shortwave feedbacks. We can see how the atmospheric emissivity changes. For example, as we change the CO2 level, the default emissivity in this model being 0.77-- the value that gives us a surface temperature about 280k, the current best estimate of Earth's surface temperature.
Finally, if we like we can vary the solar constant. We can vary the initial albedo-- Earth's planetary albedo-- which will of course be modified as we change some of the feedback factors.
So that's how it works. You're going to explore this model further in your problem set.
