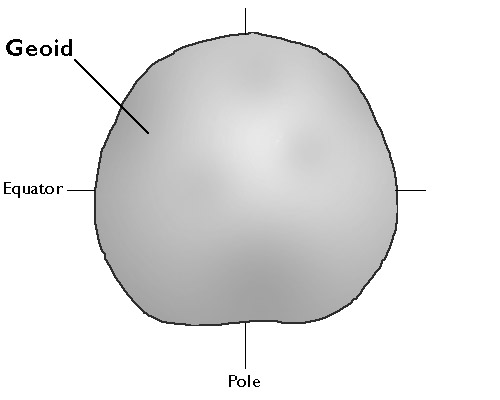
The accuracy of coordinates that specify geographic locations depends upon how the coordinate system grid is aligned with the Earth's surface. Unfortunately for those who need accurate geographic data, defining the shape of the Earth's surface is a non-trivial problem. So complex is the problem that an entire profession, called geodesy, has arisen to deal with it.
Geodesists define the Earth's surface as a surface that closely approximates global mean sea level, but across which gravity is everywhere equal. They refer to this shape as the geoid. Geoids are lumpy because gravity varies from place to place in response to local differences in terrain and variations in the density of materials in the Earth's interior. Geoids are also a little squat. Sea level gravity at the poles is greater than sea level gravity at the equator, a consequence of Earth's "oblate" shape as well as the centrifugal force associated with its rotation.
Geodesists at the U.S. National Geodetic Survey describe the geoid as an "equipotential surface" because the potential energy associated with the Earth's gravitational pull is equivalent everywhere on the surface. Like fitting a trend line through a cluster of data points, the geoid is a three-dimensional statistical surface that fits as closely as possible gravity measurements taken at millions of locations around the world. As additional and more accurate gravity measurements become available, geodesists revise the geoid periodically. Some geoid models are solved only for limited areas; GEOID03, for instance, is calculated only for the continental U.S.
Recall that horizontal datums define how coordinate system grids align with the Earth's surface. Long before geodesists calculated geoids, surveyors used much simpler surrogates called ellipsoids to model the shape of the Earth.