27. Map Projections

Latitude and longitude coordinates specify point locations within a coordinate system grid that is fitted to sphere or ellipsoid that approximates the Earth's shape and size. To display extensive geographic areas on a page or computer screen, as well as to calculate distances, areas, and other quantities most efficiently, it is necessary to flatten the Earth.

Figure 2.28.1 Map projections are mathematical equations that transform geographic coordinates (conventionally designated by the Greek symbols lambda for longitude and phi for latitude) into plane coordinates (x and y). If all the necessary parameters are known, inverse projection equations can be used to transform projected coordinates back into unprojected geographic coordinates.

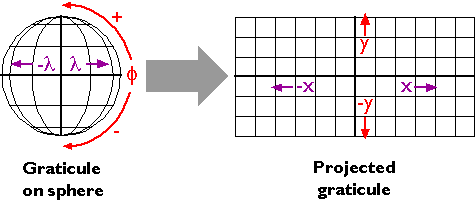
Georeferenced plane coordinate systems like the Universal Transverse Mercator and State Plane Coordinates systems (examined elsewhere in this chapter) are created by first flattening the graticule, then superimposing a rectangular grid over the flattened graticule. The first step, transforming the geographic coordinate system grid from a more-or-less spherical shape to a flat surface, involves systems of equations called map projections.

Many different map projection methods exist. Although only a few are widely used in large-scale mapping, the projection parameters used vary greatly. Geographic information systems professionals are expected to be knowledgeable enough to select a map projection that is suitable for a particular mapping objective. Such professionals are expected to be able to recognize the type, amount, and distribution of geometric distortion associated with different map projections. Perhaps most important, they need to know about the parameters of map projections that must be matched in order to merge geographic data from different sources. The pages that follow introduce the key concepts. The topic is far too involved to master in one section of a single chapter, however. Indeed, Penn State offers an entire online course in Map Projections: Spatial Reference Systems in GIS (GEOG 861). If you are or plan to become, a GIS professional, you should own at least one good book on map projections. Several recommendations follow in the bibliography at the end of this chapter.

Students who successfully complete this section should be able to:

1. interpret distortion diagrams to identify geometric properties of the sphere that are preserved by a particular projection;
2. classify projected graticules by projection family.