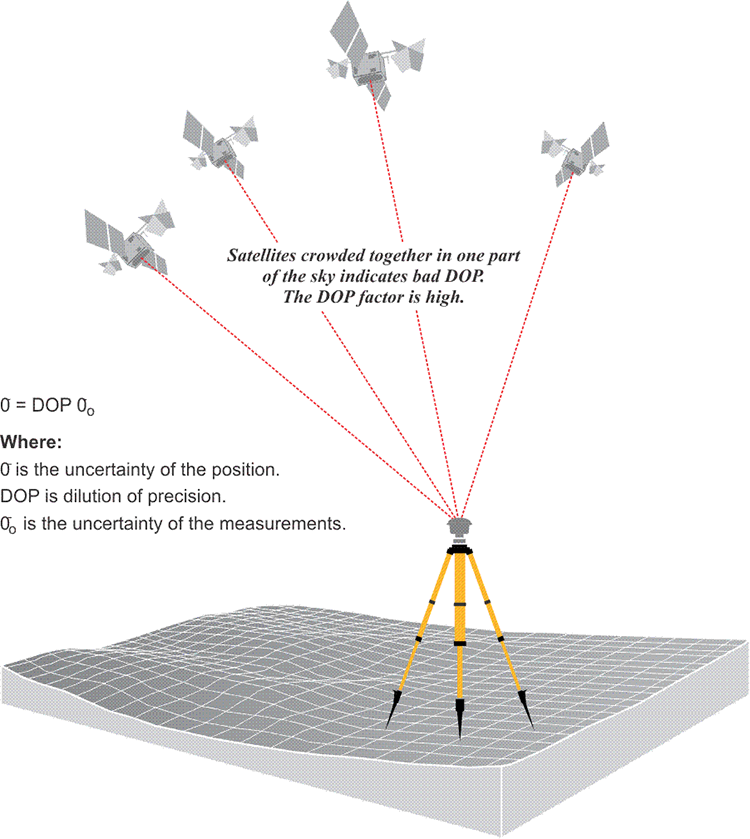
The distribution of the satellites above an observer’s horizon has a direct bearing on the quality of the position derived from them. Like some of its forerunners, the accuracy of a GPS position is subject to a geometric phenomenon called dilution of precision (DOP). This number is somewhat similar to the strength of figure consideration in the design of a triangulation network. DOP concerns the geometric strength of the figure, described by the positions of the satellites with respect to one another and the GPS receivers. A low DOP factor is good, a high DOP factor is bad. In other words, when the satellites are in the optimal configuration for a reliable GPS position, the DOP is low, when they are not, the DOP is high.
Four or more satellites must be above the observer’s mask angle for the simultaneous solution of the clock offset and three dimensions of the receiver’s position. But if all of those satellites are crowded together in one part of the sky, the position would be likely to have an unacceptable uncertainty, and the DOP, or dilution of precision, would be high. In other words, a high DOP is a like a warning that the actual errors in a GPS position are liable to be larger than you might expect. But remember, it is not the errors themselves that are directly increased by the DOP factor; it is the uncertainty of the GPS position that is increased by the DOP factor.
Now, since a GPS position is derived from a three-dimensional solution, there are several DOP factors used to evaluate the uncertainties in the components of a GPS position. For example, there is horizontal dilution of precision (HDOP) and vertical dilution of precision (VDOP) where the uncertainty of a solution for positioning has been isolated into its horizontal and vertical components, respectively. When both horizontal and vertical components are combined, the uncertainty of three-dimensional positions is called position dilution of precision (PDOP). There is also time dilution of precision (TDOP), which indicates the uncertainty of the clock. There is geometric dilution of precision (GDOP), which is the combination of all of the above. And finally, there is relative dilution of precision (RDOP), which includes the number of receivers, the number of satellites they can handle, the length of the observing session, as well as the geometry of the satellites’ configuration.
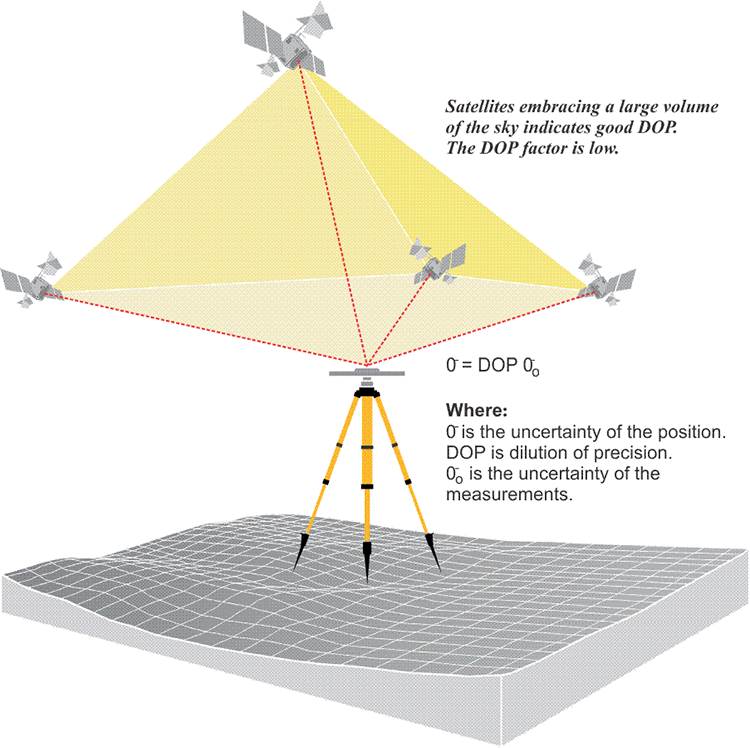
PDOP is perhaps the most common, which combines both horizontal and vertical. But the idea is very straightforward in the sense that the better the geometry, the better the intersection of the ranges from the satellites, the lower that the dilution of precision value will be and the better the position derived will be. This is a very practical consideration in GPS work.
The user equivalent range error (UERE) is the total error budget affecting a pseudorange. It is the square root of the sum of the squares of the individual biases discussed in Chapter 2. Using a calculation like that mentioned, the PDOP (position dilution of precision) factor can be used to find the positional error that will result from a particular UERE at the one sigma level (68.27%). For example, supposing that the PDOP factor is 1.5 and the UERE is 6 m, the positional accuracy would be 9 m at the 1 sigma level (68.27%). In other words, the standard deviation of the GPS position is the dilution of precision factor multiplied by the square root of the sum of the squares of the individual biases (UERE). Multiplying the 1 sigma value times 2 would provide that 95% level of reliability in the error estimate, which would be 18 m.
The size of the DOP factor is inversely proportional to the volume of the tetrahedron described by the satellites' positions and the position of the receiver. The larger the volume of the body defined by the lines from the receiver to the satellites, the better the satellite geometry and the lower the DOP. An ideal arrangement of four satellites would be one directly above the receiver, the others 120° from one another in azimuth near the horizon. With that distribution, the DOP would be nearly 1, the lowest possible value. In practice, the lowest DOPs are generally around 2. The mask angle plays a part here. If you had four satellites, and three of them were at the horizon and one was directly overhead, this would be a very low dilution of precision value. However, you wouldn't want to track satellites that were right against the horizon. You want them above this mask angle, 10 or 15 degree mask angle, to try to minimize the effect of the ionosphere. The users of most GPS receivers can set a PDOP mask to guarantee that data will not be logged if the PDOP goes above the set value. A typical PDOP mask is 6. As the PDOP increases, the accuracy of the pseudorange positions probably deteriorate, and as it decreases, they probably improve. When a DOP factor exceeds a maximum limit in a particular location, indicating an unacceptable level of uncertainty exists over a period of time, that period is known as an outage. This expression of uncertainty is useful both in interpreting measured baselines and planning a GPS survey.