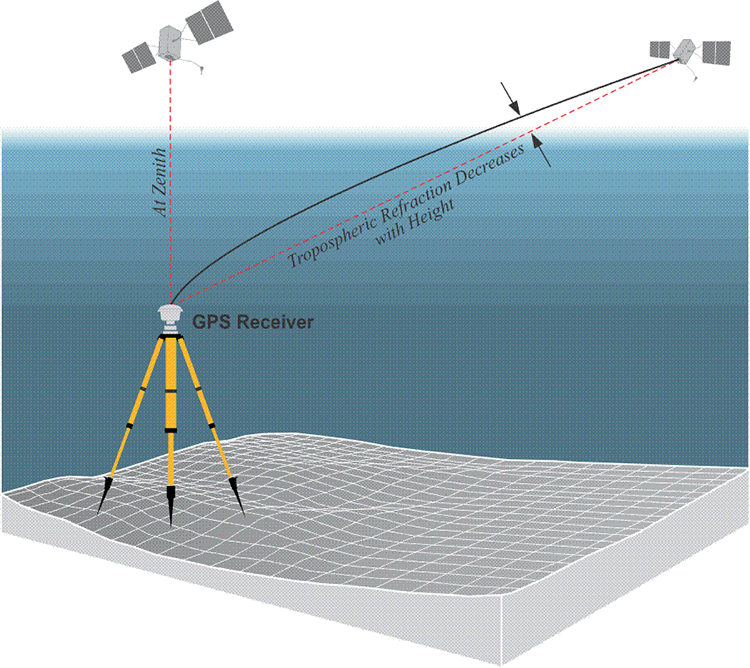
Troposphere
The troposphere is that part of the atmosphere closest to the earth. It extends from the surface to about 9 km over the poles and about 16 km over the equator, but in this work, it will be combined with the tropopause and the stratosphere, as it is in much of GPS literature. Therefore, the following discussion of the tropospheric effect will include the layers of the earth’s atmosphere up to about 50 km above the surface. While the troposphere is no more cooperative than the ionosphere in terms of being consistent, the troposphere and the ionosphere are by no means alike in their effect on the satellite’s signal. The troposphere is refractive, its refraction of a GPS satellite’s signal is not related to its frequency. The refraction is tantamount to a delay in the arrival of a GPS satellite's signal. It can also be conceptualized as a distance added to the range the receiver measures between itself and the satellite. The troposphere is part of the electrically neutral layer of the earth’s atmosphere, meaning it is not ionized. The troposphere is also nondispersive for frequencies below 30 GHz or so. Therefore, L1, L2, and L5 are equally refracted. This means that the range between a receiver and a satellite will be shown to be a bit longer than it actually is. However, as it is in the ionosphere, density affects the severity of the delay of the GPS signal as it travels through the troposphere. For example, when a satellite is close to the horizon, the delay of the signal caused by the troposphere is maximized. The tropospheric delay of the signal from a satellite at zenith, directly above the receiver, is minimized.
Satellite elevation and tropospheric effect.
The situation is analogous to atmospheric refraction in astronomic observations; the effect increases as the energy passes through more of the atmosphere. The difference in GPS is that it is the delay, not the angular deviation caused by the changing density of the atmosphere, that is of primary interest. The GPS signal that travels the shortest path through the troposphere will be the least delayed by it. In other words, there is less tropospheric delay when the satellite is at the zenith of the receiver.
Modeling. Modeling the troposphere is one technique used to reduce the bias in GPS data processing, and it can be up to 95% effective. However, the residual 5% can be quite difficult to remove. Several a priori models have been developed, for example, the Saastamoinen model and the Hopfield models, which perform well when the satellites are at reasonably high elevation angles. However, it is advisable to limit GPS observations to those signals above 15% or so to ameliorate the effects of atmospheric delay.
The dry and wet components of refraction.
Refraction in the troposphere has a dry component and a wet component. The dry component which contributes most of the delay, perhaps 80% to 90%, is closely correlated to the atmospheric pressure. The dry component can be more easily estimated than the wet component. It is fortunate that the dry component contributes the larger portion of range error in the troposphere, because the size of the delay attributable to the wet component depends on the highly variable water vapor distribution in the atmosphere. Even though the wet component of the troposphere is nearer to the Earth’s surface, measurements of temperature and humidity are not strong indicators of conditions on the path between the receiver and the satellite. While instruments that can provide some idea of the conditions along the line between the satellite and the receiver are somewhat more helpful in modeling the tropospheric effect, the high cost of sending water vapor radiometers and radiosondes aloft generally restricts their use to only the most high-precision GPS work. In most cases, this aspect must remain in the purview of mathematical modeling; such calculations include a hydrostatic model with corrections and a horizontal gradient component. It is important to recognize that the index of tropospheric refraction decreases as height increases.