The Navigation Solution

Absolute (aka Autonomous, aka Single Point) Solution

Source: GPS for Land Surveyors

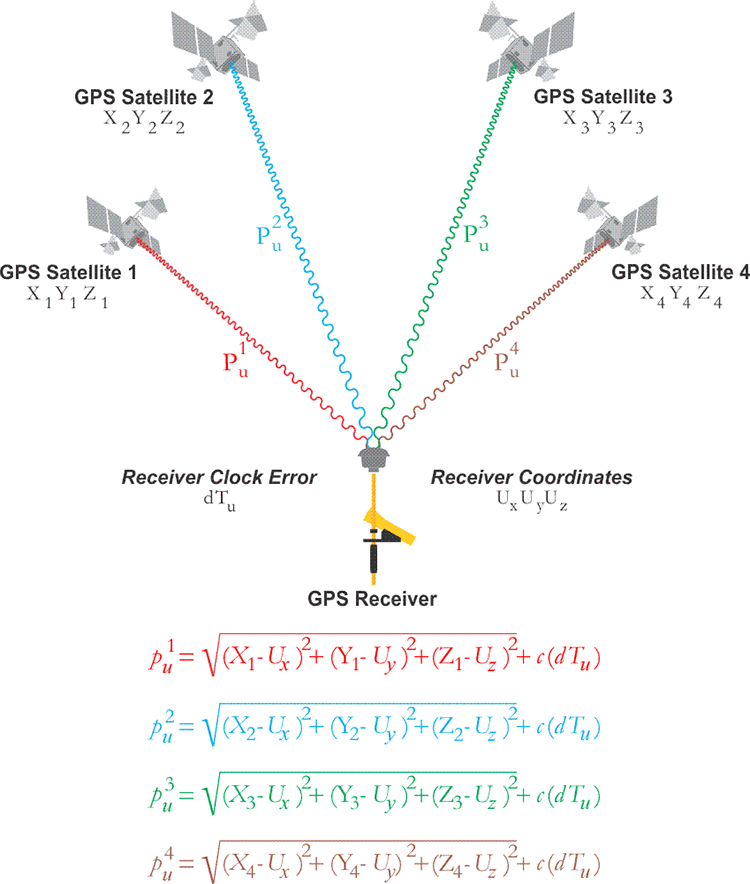
Another type of point positioning is known as absolute positioning, single-point positioning, or the Navigation solution. It is characterized by a single receiver measuring its range to a minimum of four satellites simultaneously. An autonomous GPS positioning is not post-processed, and there is really no communication with a station that's on a known point. In other words, autonomous positioning is not differential (relative); the receiver is operating independently. As always, four satellites are required, as indicated here. The receiver is on an unknown position and must solve for its own receiver clock error. It needs to solve for x, y, z, and time. The Navigation solution is, in one sense, the fulfillment of the original idea behind GPS. It relies on a coded pseudorange measurement and can be used for virtually instantaneous positioning. In this method, the positions of the satellites are available from the data in their broadcast ephemerides. The satellite clock offset, and the ionospheric correction are also available from the Navigation messages of all four satellites.  As you know, these corrections from that message are not ideal.  Even if all the data in the navigation message contained no errors, and they surely do, four unknowns remain: the position of the receiver in three Cartesian coordinates, u_x , u_y , and u_z , and the receiver’s clock error dT_u . Three pseudoranges provide enough data to solve for u_x , u_y , and u_z . And the fourth pseudorange provides the information for the solution of the receiver’s clock offset. The ability to measure dT, the receiver’s clock error, is one reason the moderate stability of quartz crystal clock technology is entirely adequate as a receiver oscillator. A unique solution is found here because the number of unknowns is not greater than the number of observations. The receiver tracks a minimum of 4 satellites simultaneously; therefore, these four equations can be solved simultaneously for every epoch of the observation. An epoch in GPS is a very short period of observation time (i.e. 1 second or perhaps less), and is generally just a small part of a longer measurement. However, theoretically, there is enough information in any single epoch to solve these equations. This is the reason the trajectory of a receiver in a moving vehicle can be determined by this method. With 4 satellites available, resolution of a receiver’s position and velocity are both available through the simultaneous solution of these four equations.