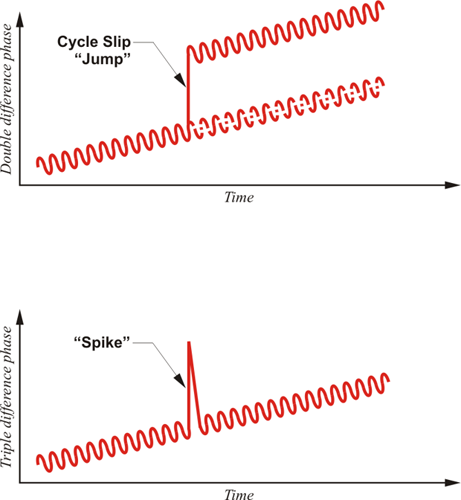
Here's a graphic to give the idea of a cycle slip. As you see here, the cycle slip is indicated in a double difference, here, as a jump from one place to another. And in a triple difference, it's a spike.
A cycle slip is a discontinuity in a receiver’s phase lock on a satellite’s signal. A power loss, a very low signal-to-noise ratio, a failure of the receiver software, a malfunctioning satellite oscillator can cause a cycle slip. It can also be caused by severe ionospheric conditions. Most common, however, are obstructions such as buildings, trees, etc., that are so solid they prevent the satellite signal from being tracked by the receiver. Under such circumstances, when the satellite reappears, the tracking resumes.
Coded pseudorange measurements are not as affected by cycle slips as are carrier phase measurements. On the other hand, carrier phase positioning accuracy suffers if cycle slips are not detected and repaired. A cycle slip causes the critical component for successful carrier phase positioning, a resolved integer cycle ambiguity, N, to become instantly unknown again. In other words, lock is lost. When that happens, correct positioning requires that N be reestablished.
There are several methods of handling cycle slips. They are often controlled in post-processing rather than real-time.
Repairing Cycle Slips
In post-processing, the location and their size of cycle slips must be determined; then the data set can be repaired with the application of a fixed quantity to all the subsequent phase observations. One approach is to hold the initial positions of the stations occupied by the receivers as fixed, and edit the data manually. This has proven to work, but would does try patience. Another approach is to model the data on a satellite-dependent basis with continuous polynomials to find the breaks and then manually edit the data set a few cycles at a time. In fact, several methods are available to find the lost integer phase value, but they all involve testing quantities.
One of the most convenient of these methods is based on the triple difference. It can provide an automated cycle slip detection system that is not confused by clock drift and, once least-squares convergence has been achieved, it can provide initial station positions even using the unrepaired phase combinations. They may still contain cycle slips, but the data can nevertheless be used to process approximate baseline vectors. Then the residuals of these solutions are tested, sometimes through several iterations. Proceeding from its own station solutions, the triple difference can predict how many cycles will occur over a particular time interval. Therefore, by evaluating triple difference residuals over that particular interval, it is not only possible to determine which satellites have integer jumps, but also the number of cycles that have actually been lost. In a sound triple difference solution without cycle slips, the residuals are usually limited to fractions of a cycle. Only those containing cycle slips have residuals close to one cycle or larger. Once cycle slips are discovered, their correction can be systematic.
For example, suppose the residuals of one component double difference of a triple-difference solution revealed that the residual of satellite PRN 16 minus the residual of satellite PRN 17 was 8.96 cycles. Further, suppose that the residuals from the second component double difference showed that the residual of satellite PRN 17 minus the residual of satellite PRN 20 was 14.04 cycles. Then, one might remove 9 cycles from PRN 16 and 14 cycles from PRN 20 for all the subsequent epochs of the observation. However, the process might result in a common integer error for PRNS 16, 17, and 20. Still, small jumps of a couple of cycles can be detected and fixed in the double-difference solutions. In other words, before attempting double difference solutions, the observations should be corrected for cycle slips identified from the triple difference solution. And even though small jumps undiscovered in the triple difference solution might remain in the data sets, the double difference residuals will reveal them at the epoch where they occurred. However, some conditions may prevent the resolution of cycle slips down to the one-cycle level. Inaccurate satellite ephemerides, noisy data, errors in the receiver’s initial positions, or severe ionospheric effects all can limit the effectiveness of cycle-slip fixing. In difficult cases, a detailed inspection of the residuals might be the best way to locate the problem.