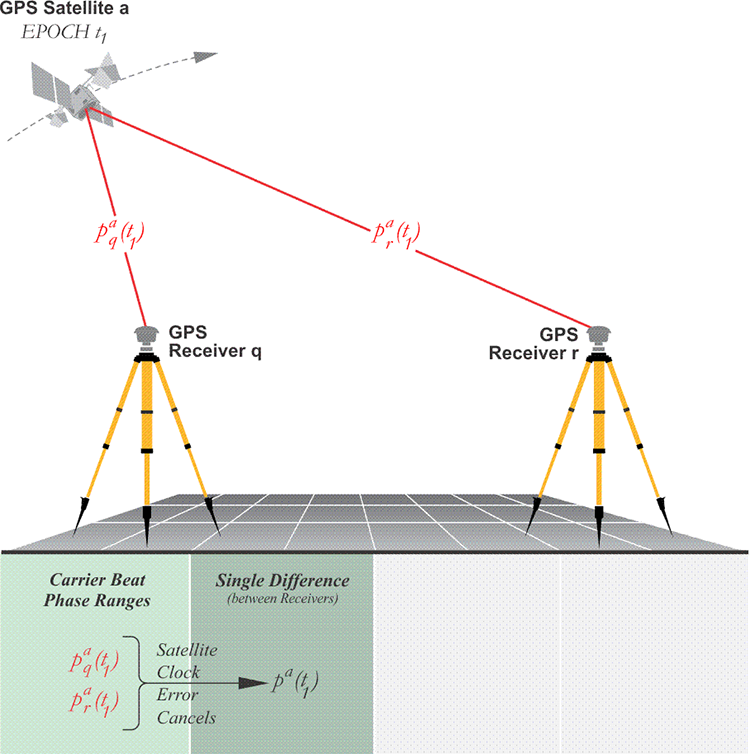
Please recall that the biases in both the pseudorange and the carrier phase equations discussed at the top obscure the true geometric ranges between the receivers to the satellites, which then contaminate the measurement of the baseline between the receivers. In other words, to reveal the actual vectors between two or more receivers used in relative positioning, those errors must be diminished to the degree that is possible. Fortunately, some of those embedded biases can be virtually eliminated by combining the simultaneous observables from the receivers in processes known as differencing. Even though the noise is increased by a factor of two with each differencing operation, it is typically used in commercial data processing software for both pseudorange and carrier phase measurements. There are three types of differencing, the single difference, double difference, and triple difference. Within the single difference category, there are the between-receivers single difference and the between-satellites single difference. Both require that all the receivers observed the same satellites at the same time. In GPS, the word differencing has come to represent several types of simultaneous baseline solutions of combined measurements. One of the foundations of differencing is the idea of the baseline as it is used in GPS. For example, a single difference, also known as a between-receivers difference, can refer to the difference in the simultaneous carrier phase measurements from one GPS satellite as measured by two different receivers. In the illustration, there are two receivers —q and r— observing the same satellite.
Between-Receivers Single Difference
A between-receivers single difference reduces the effect of biases, even though it doesn’t eliminate them. Since the two receivers are both observing the same satellite at the same time, the difference between the satellite clock bias, dt, at the first receiver and dt at the second receiver, Δdt, is obviously zero. Also, since the baseline is typically short compared with the 20,000-km altitude of the GPS satellites, the atmospheric biases and the orbital errors, i.e., ephemeris errors, recorded by the two receivers at each end are similar. This correlation obviously decreases as the length of the baseline increases. Generally speaking, this correlation allows centimeter level carrier phase positioning with baselines up to 10 km or so, and meter level positioning with baselines of a few hundreds of kilometers using pseudorange observations.
The between-receivers single difference provides better position estimates for the receivers by subtracting, differencing, each receiver’s observation equation from the other. For example, if one of the receivers is a base standing at a control station whose position is known, it follows that the size of the positional error of the receiver there is knowable. Therefore, the positional error at the other end of the baseline can be estimated by finding the difference between the biases at the base and the biases at the rover. Corrections can then be generated which can reduce the three-dimensional positional error at the unknown point by reducing the level of the biases there. It is primarily this correlation and the subsequent ability to reduce the level of error that distinguishes differenced relative positioning from single point positioning.
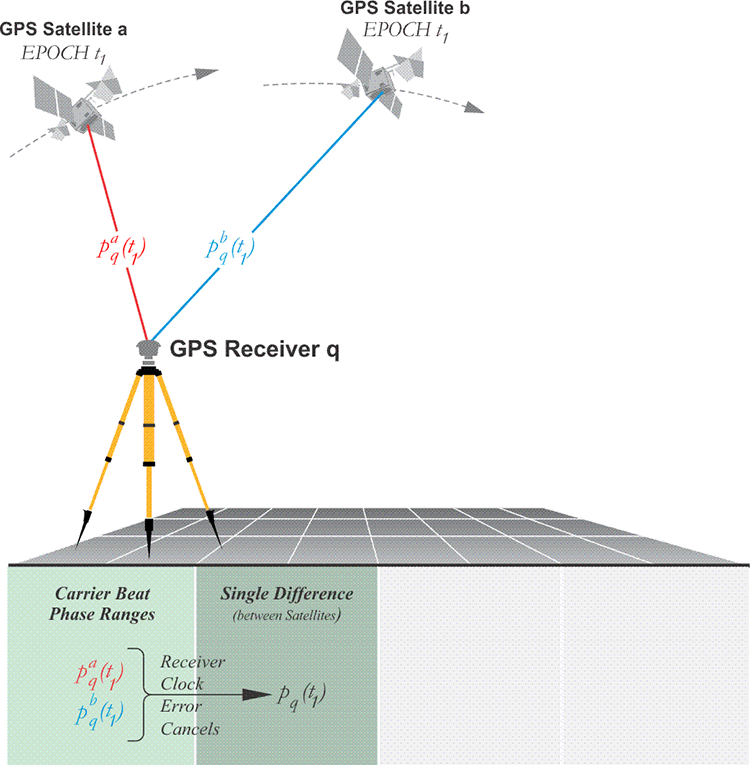
The between-satellites single difference involves a single receiver observing two GPS satellites simultaneously and the code and/or phase measurement of one satellite are differenced, subtracted, from the other. The data available from the between-satellites difference allows the elimination of the receiver clock error because there is only one involved. And the atmospheric effects on the two satellite signals are again nearly identical as they come into the lone receiver, so the effects of the ionospheric and tropospheric delays are reduced. However, unlike the between-receivers single difference, the between-satellites single difference does not provide a better position estimate for the receiver involved. In fact, the resulting position of the receiver is not better than would be derived from single point positioning.
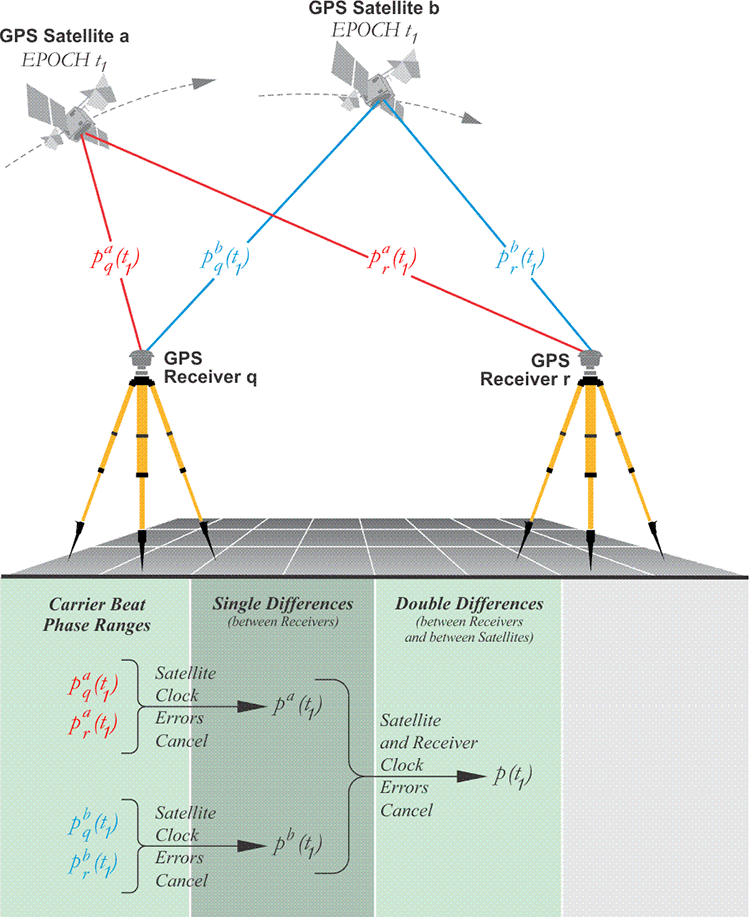
When the two types of single differences are combined, the result is known as a double difference. A double difference can be said to be a between-satellite single difference of a between-receiver single difference. The improved positions from the between-receiver single difference step are not further enhanced by the combination with the between-satellite single difference. Still, including the between-satellite single difference is useful because the combination virtually eliminates clock errors, both the satellite and receiver clock errors. The removal of the receiver clock bias in the double difference makes it possible to segregate the errors attributable to the receiver clock biases from those from other sources. This segregation improves the efficiency of the estimation of the integer cycle ambiguity in a carrier phase observation, N. In other words, the reduction of all the non-integer biases makes the computation of the final accurate positions more efficient.
The double difference, for all practical purposes, has eliminated the receiver clock errors and the satellite clock errors. This is used in most GPS post-processing and software. The integer ambiguity, N, still remains with the carrier phase observation.
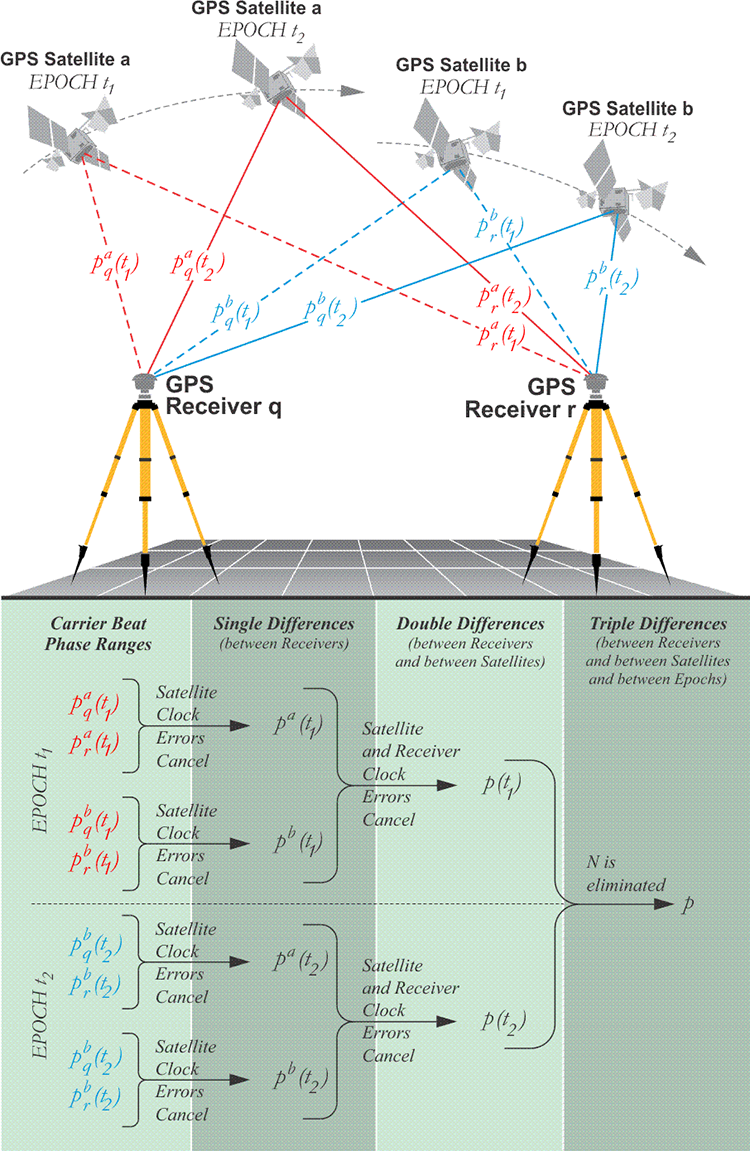
A triple difference is the difference of two double differences over two different epochs. The triple difference has other names. It is also known as the receiver satellite-time triple difference and the between-epochs difference. Triple differencing serves as a good pre-processing step, because it can be used to detect and repair cycle slips.