Interpreting Contour Maps

Read...

Topographic map of Hawaii with point "P" labeled. Contours are drawn every 1,000 feet.

Credit: David Babb

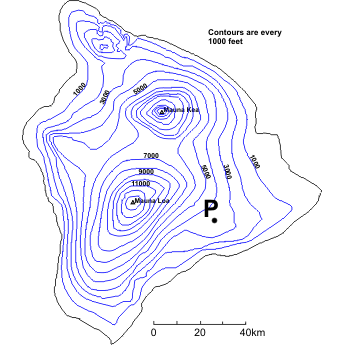
Meteorologists regularly use contour maps to see how weather variables (temperature or pressure, for example) change over large areas, but they also use them to estimate values of weather variables at individual points. To get us started on interpreting contour maps, we're first going to revisit our topographic map of Hawaii (right).

How would we go about figuring out the elevation of the point marked "P"?  First, we must identify the two contours that lie on either side of "P."  In some cases the contours that we need are clearly labeled; however, in other instances, you will need to use the contour interval (1,000 feet, in this case) to "count" up or down from a labeled contour. On our map, point "P" lies between 3000 feet and 4000 feet contours, so the elevation at point "P" is greater than (but not equal to) 3000 feet but less than (but again, not equal to) 4000 feet. We know that point "P" is not equal to either of these values because it does not lie on one of the contour lines.

Technically, this is all that we can say for sure about the elevation at point "P" -- it can be anywhere between 3,000 and 4,000 feet. However, often instead of giving a range of elevation, we would prefer a single number. In such cases, we can interpolate (make an estimate by assuming the elevation changes linearly) between the two known contours. In this case, we can see that point "P" is about half-way between the two contours and thus has an elevation of approximately 3,500 feet. Using interpolation usually provides us with a sufficient approximation, but we must always realize that it's only an estimate.

What about closed contours that have no other contours drawn within them? Look again at the contour map and focus your attention on the southern-most peak, Mauna Loa. How might we estimate the height of this peak? Clearly, we do not have two contours to use... or do we? The last drawn contour is 13,000 feet. This means that the peak is higher than 13,000 feet. However, we know that the summit of Mauna Loa is not higher than 14,000 feet. Why? Well, if it were, then the 14,000 feet contour would have been drawn around the summit. So, for an inner-most closed contour, the range is always between the last drawn contour and the next undrawn contour. You should also note that interpolation cannot be performed in such cases because we have no way of knowing how far away the undrawn contour is. The summit of Mauna Loa is 13,452 ft (within our deduced range of 13,000-14,000 feet), but we really couldn't have known that just from our topographic map (unless the peak elevation was labeled).

Two variables that are commonly contoured by meteorologists are temperature and air pressure. Isopleths of temperature are called isotherms (contours of constant temperature), and isopleths of pressure are called isobars (contours of constant pressure). Don't confuse the two! It would be incorrect to look at a map that shows only contours of constant temperature and call them "isobars," for example.

Maps with isobars of sea-level pressure help meteorologists recognize areas of high and low pressure. Why is this important? Well, generally speaking, areas of high pressure at the surface are often areas of "fair" weather (relatively calm, with at least some sunshine). Meanwhile, regions of low pressure are often somewhat unsettled (cloudy with precipitation). To see a map with isobars of sea-level pressure, check out the image below, from 15Z on May 1, 2017.

Analysis of sea-level isobars (contours of constant pressure) at 15Z on May 1, 2017.

Credit: University of Illinois

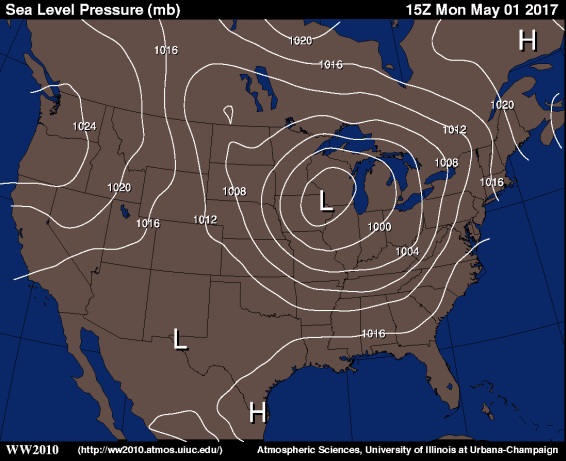
The H's mark centers of high pressure (highest pressure in the region), while the L's mark centers of low pressure (lowest pressure in the region). The feature that would immediately jump out at a weather forecaster as a region of "active" weather is the large area of low pressure centered over the Midwest (near the Iowa / Wisconsin border).

The first step in interpreting values from this image is to figure out the contour interval, which is four millibars (millibars is a standard unit of pressure). Knowing that, we can estimate the pressure near the center of the low over the Midwest. The inner-most closed isobar is 996 millibars (it's unlabeled, but it's inside of the 1000 millibar isobar and values are decreasing toward the center of the low), so the pressure must be less than 996 millibars. However, there's no 992 millibar isobar drawn, so the pressure must be greater than 992 millibars.

Similarly, meteorologists contour maps of temperature because such maps allow them to easily spot areas of cold and warm air. But, maps of isotherms are often color-coded to help make the interpretation easier (for what it's worth, colors are sometimes used on topographic maps, too). I caution you that color schemes and contour intervals can vary widely on images you may see on television or online, and determining which color is which can sometimes be a real challenge. But, if you understand how to interpret contour maps, you can keep your wits about you and use the isotherms (in conjunction with the colors, if you'd like) to gather useful information.

For example, check out the map of isotherms at 15Z on May 1, 2017, below. The contour interval on the image is 5 degrees Fahrenheit. Given that, what would you say is an appropriate range in temperature for somewhere in Indiana? Given that the 60 degree Fahrenheit isotherm and 55 degree Fahrenheit isotherm nearly match the eastern and western borders of the state (respectively), it's fair to say that temperatures in Indiana were greater than 55 degrees Fahrenheit, but less than 60 degrees Fahrenheit. And, if you look at the color key on the right of the image, the shade of yellow-green (or is it green-yellow?) over Indiana matches the color used for temperatures between 55 and 60 degrees Fahrenheit (although some might find it hard to tell).

Analysis of surface isotherms (contours of constant temperature) at 15Z on May 1, 2017.

Credit: University of Illinois

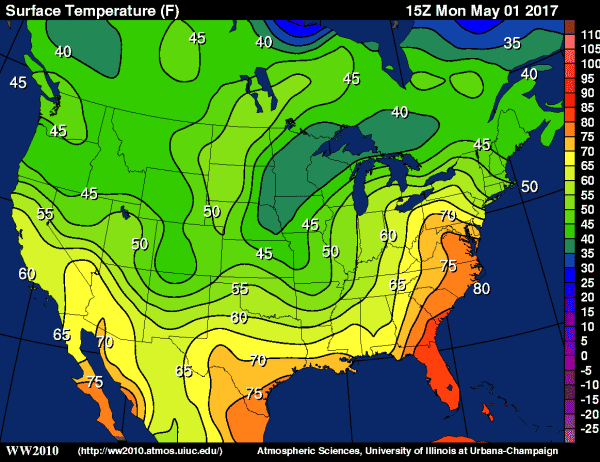
If we wanted to pick a specific point, "P," on the map, near Indianapolis, Indiana, and estimate a specific temperature, we could do that, too. Point "P" is approximately half-way between the 55 and 60 degree Fahrenheit isotherms, so the temperature at "P" is about half-way between 55 and 60 degrees Fahrenheit. We'll call it 57 or 58 degrees Fahrenheit, knowing that we're just making our best estimate based on the isotherms.

I should also point out that sometimes you won't even see isotherms plotted, and instead, a temperature map will just be shaded. In reality, every boundary where colors change is an isotherm (even if it's not drawn or labeled), and sometimes very small contour intervals are used. On such maps, like this analysis of temperatures from 17Z on May 24, 2017. Using the color key is the only way to go, and even then (because colors change every degree in this case), estimating a specific temperature at a point can be difficult when the shadings are so similar.

To see a few more examples of interpreting values from a contour map, watch the short video (3:28) below.

Finally, before you continue on, make sure to check the Key Skill and Quiz Yourself sections below. They'll help you make sure that you can interpret contour maps on your own, which is a useful skill outside of meteorology, too (elevation and many other variables can be isoplethed, and the principle for interpreting the values is the same, regardless of what's being plotted).