Prioritize...
At the completion of this section, you should be able to discuss the meaning of an "apparent force" and how apparent forces are created. You should also be able to discuss the Coriolis force, specifically what causes it, what determines its magnitude, what its effects are, and the time/space scales on which its effects are visible (and not visible).
Read...
Perhaps the title of this section has you a bit puzzled. What exactly is an "apparent" force? Well, "real" forces like the pressure-gradient force, can cause motion. But, we perceive some forces because of motion (these are "apparent forces"). Yes, perception is important when it comes to apparent forces, and to see what I mean, check out this time lapse of the sky over Penn State's Beaver Stadium from August 21, 2017. After a vibrant sunrise, you can watch the sun move across the sky. To us here on Earth, it looks like the sun is moving. But, is that what's really going on? Of course not! The earth revolves around the sun, and we're the ones moving, not the sun.
So, even though we perceive the sun moving across the sky, it's a false perception that arises from our frame of reference. By frame of reference, I mean the part of your immediate surroundings that you sense is not moving. Indeed, if you're standing still on earth, you perceive that you're not moving, but you're really flying through space at about 10,000 miles per hour along with the earth!
Our frames of reference give rise to "apparent" forces, too. For example, did you know that you accelerate every time you drive around a curve in a car (even if you keep your speed constant)? Acceleration, by definition, is a change in in a velocity vector, which means any change in speed or direction is an acceleration. There's an acceleration toward the center of the curve, but you perceive that your car is not accelerating as it negotiates the curve at constant speed. This perception leads you to falsely sense that some force, which acts to pull your body outward, is at work (more so if you're going too fast around the curve). But, this outward-accelerating force, called the "centrifugal force," is only an "apparent" force that arises from the false impression that the car's interior is not accelerating. If you've ever gone on a "tilt-a-whirl" type of ride at an amusement park (like the one below) you've felt the centrifugal force at work!

So, the fact that we falsely sense that our earthly surroundings are unaccelerated has big impacts for how we perceive the world around us, and that's a big issue when it comes to assessing the movement of air. Specifically, an apparent force, called the "Coriolis force" has a real impact on our observations of the direction of the wind.
Coriolis Force
Remember that I demonstrated the consequences of the pressure gradient force using a two-compartment water tank. In that experiment, water flowed directly from high to low pressure over a short period of time. Air behaves much the same way on small time and spatial scales (for example, letting the air out of a balloon). On the much longer time scales and much larger spatial scales of high and low pressure systems, air does not flow directly toward low pressure. For example, check out the 18Z surface analysis on September 8, 2011 (below). Focus your attention on the closed, circular isobars and the wind barbs around Tropical Storm Lee (its center was just off the central coast of Louisiana at this time). Note that the winds don't blow directly toward the lowest pressure located at the center, so the pressure-gradient force must not be the only force at work.
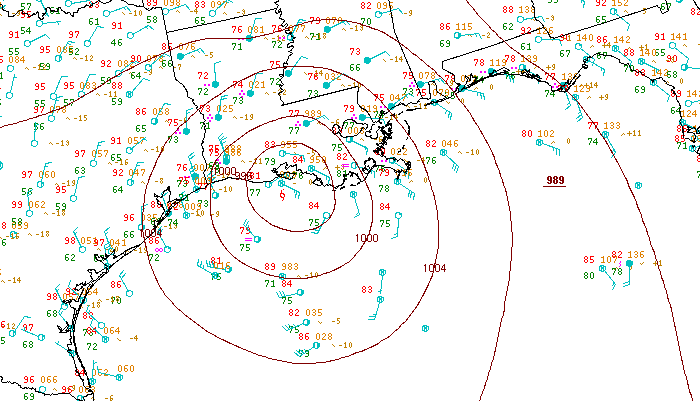
What is this mysterious force that prevents air from moving directly inward toward the center of lowest pressure? It's the Coriolis force, which, like the centrifugal force, is an "apparent" force. Indeed, the Coriolis force arises simply as a consequence of the eastward rotation of our spherical earth. The Coriolis force is named after the French engineer and mathematician, Gustave Coriolis, who actually didn't study the effects of the rotating earth at all. He noticed the apparent force that would later be named after him during his work with rotating parts of machines.
So, how does the Coriolis force come into play in the atmosphere? Let's consider two points at the same longitude, one at latitude 40 degrees north (we'll call Point N) and the other at 20 degrees north (Point S). Because the latitude circle at 40 degrees north is noticeably smaller than the latitude circle at 20 degrees north, Point S must move eastward faster than Point N because it must travel a greater distance around the equatorial circle during one 24-hour revolution of the earth. Indeed, Point S moves at approximately 900 miles per hour, while, at 40 degrees North latitude, the eastward speed of Point N (and all other points at 40 degrees north) is about 800 miles per hour. For sake of reference, the eastward speed at the North Pole is zero.
Peculiar things happen when points on the earth's surface move at different speeds as the planet rotates on its axis. Suppose a projectile is launched directly northward from the equator toward latitude 40 degrees north. The projectile retains its great eastward speed as it starts its northward journey. With each passing moment, the northward-moving projectile moves over ground that has an eastward speed less than its own. In effect, the projectile surges east ahead of the lagging ground below. To an observer on the launching pad, the projectile appears to swerve to the right as a natural consequence of our spherical, rotating earth.

Launching the projectile from north to south results in a similar rightward deflection relative to the observer on the launching pad at 40 degrees north. The projectile, by retaining much of its original eastward speed of about 800 miles an hour, moves progressively over ground with faster eastward speed. In effect, the projectile falls behind the ground below, lagging increasingly to the west. To the observer on the launching pad at latitude 40 degrees north, the projectile again appears to deflect to the right. The bottom line is that no matter what direction the observer launches the projectile, the deflection will always be to their right in the Northern Hemisphere. I can make similar arguments for the Southern Hemisphere by first noting that if an observer in space looks "up" at the South Pole, the sense of the Earth's rotation appears to be clockwise, which is the opposite of the counterclockwise sense an observer gets while looking "down" at the North Pole. You can contrast the two in this animation showing each perspective. Thus, deflections due to the Coriolis force in the Southern Hemisphere are to the left of the observer.
I've used an object moving north-south to demonstrate the impacts of the Coriolis force because I think it's the easiest to visualize. But, rest assured, Coriolis deflections to the right in the Northern Hemisphere (left in the Southern Hemisphere) occur regardless of the direction of motion. Coriolis deflections even occur for objects moving due east or due west, but I'll spare you the explanation (it's more abstract and harder to visualize than the north-south case).
Coriolis Force Effects (and Myths)
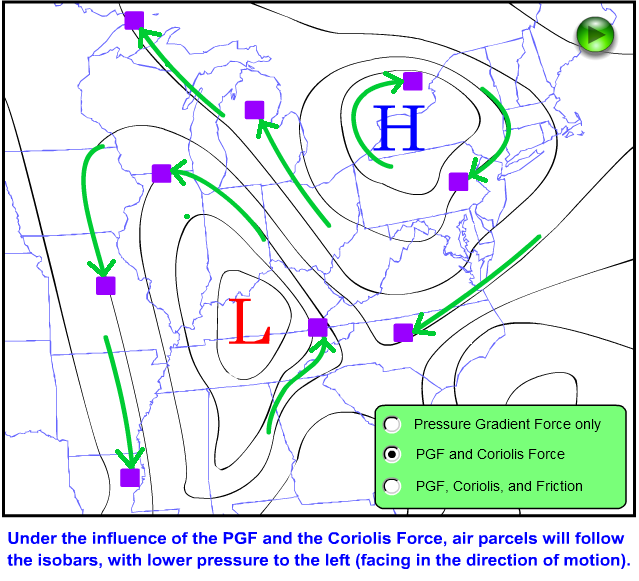
I emphasize that the Coriolis force is not a true force in the tradition of gravity or the pressure gradient force. It cannot cause motion. Rather, it is an apparent effect that simply results from an object moving over our spherical, rotating planet. The Coriolis force does not discriminate, either. Indeed, no free-moving object, including wind and water, is exempt from its influence. Given enough time, the Coriolis force causes air to move 90 degrees to the right of its initial motion caused by the pressure-gradient force. So, that means instead of air parcels crossing isobars directly from higher to lower pressure (as would happen if the pressure-gradient force was the only force acting), the combination of the Coriolis force and the pressure-gradient force causes air to move parallel to local isobars, counterclockwise around low pressure and clockwise around high pressure in the Northern Hemisphere (as depicted by the air parcel traces in the idealized weather map below). In the Southern Hemisphere, the circulation around highs and lows is reversed (it's clockwise around lows and counterclockwise around highs).
However, the magnitude of the Coriolis deflection depends on a number of factors. These factors depend on 1) the latitude of the moving object, 2) the object's velocity, and 3) the object's flight time. Its impact on air movement is clear because air moves over long distances for long periods of time. But, what about the impact of the Coriolis force on shorter events that happen on smaller scales? You may have heard that the Coriolis force determines the rotation of water swirling down a drain, or perhaps you've heard that the Coriolis force has a big impact on sporting events (like a baseball thrown from the pitcher's mound to home plate). Are these things true?
To begin to answer these questions, let's see how these three factors impact the magnitude of the Coriolis force:
- the magnitude of the Coriolis force increases with increasing latitude (closer to the poles) and is zero at the equator.
- the magnitude of the Coriolis force increases with increasing velocity of the object (or air parcel)
- the magnitude of the Coriolis force increases with increasing flight time (for the velocities typically observed in nature, a flight time of minutes to hours is typically required to observe any deflection at all)
So, what's the upshot of these factors? Well, you typically cannot observe the Coriolis deflection of water emptying from a drain (the speed is too slow and the time is too short), for starters. This is also true of water swirling down a toilet bowl. Water circulates in a certain direction because the basin is designed to move water in that direction (as the case for toilets) or the swirling water is simply residual motion left-over from filling the basin. I point to these specific examples because they are often misunderstood in popular culture. Many videos on the Internet claim to show the Coriolis Effect via water draining out of a basin, such as this video taken in Equatorial Kenya. This "experiment" has numerous problems (like using a different bowl in each case, for example), but the water draining from these small bowls occurs over too short a time for the Coriolis force to have a noticeable effect. Furthermore, at very low latitudes (right near the equator), remember that the magnitude of the Coriolis force is practically zero! Such video demonstrations are full of nonsense and bad science.

What about objects that move faster? I'll spare you the math, but let's see what the Coriolis force does to a 100 mph fast ball thrown from the pitcher's mound to home plate at Citizen's Bank Park in Philadelphia, Pennsylvania (near 40 degrees North latitude). At that speed, it takes the pitch about 0.4 seconds to reach home plate. Using these values, the Coriolis deflection is only 0.39 millimeters (0.015 inches)! That's far too small for anyone to see with the naked eye (or for any hitter to try to account for). How about a bullet fired at a long-distance target from a competition rifle? If we assume we're at 40 degrees North again, a bullet traveling 800 meters per second over a distance of 1,000 yards (0.57 miles) would have a flight time of 1.14 seconds and a Coriolis deflection of just 2.22 inches.
The "take away" point here is that although the Coriolis force affects all free-moving objects, these affects can be really small (perhaps undetectable), unless the speeds are very great or the travel time is long. The atmosphere has the advantage when it comes to the latter because air moves over long distances for long periods of time, and the Coriolis deflection becomes significant over the course of hours or days. So, when estimating wind direction we will need to consider both the pressure-gradient force as well as the Coriolis force. But, there's one more force that has important impacts near the surface of the earth that we have yet to tackle. Read on.