Prioritize...
At the end of this section you should be able to describe how the pressure-gradient force, the Coriolis force, and friction act to determine the wind direction and speed. You should be able to define the geostrophic wind, and be able to determine the geostrophic wind and surface wind directions given a map of sea-level pressures.
Read...
Now that we've learned about all of the forces that play a role in determining the speed and direction of the wind, let's see how they all work together. Ultimately, the air's motion depends on the sum of the forces that act on it, so to examine the movement of the air we'll consider a sample "parcel" of air released in a uniform pressure field in the Northern Hemisphere, and examine how each force impacts the air parcel. To do so, we'll look at this interactive force diagram (keep the window open for the duration of our discussion), which will help you see the effects of adding various forces to a parcel of air. By convention, I'll use arrows to keep track of the pressure-gradient force, friction, the Coriolis force, and the parcel's velocity.
When you first open the interactive force diagram, only the pressure gradient force (PGF) is acting (the Coriolis force and friction are turned off. Leave it that way for now). Change the magnitude of the pressure-gradient force and watch how the spacing of the isobars changes. Also notice that the parcel's velocity increases (the velocity arrow gets bigger) as the pressure-gradient force increases. Conversely, the velocity decreases as the pressure-gradient force decreases. At this point, the velocity vector points northward, blowing directly from higher to lower pressure, which is unrealistic, because we know other forces are at work.

Now let's add the contribution of the Coriolis force (make sure friction is "off"). Remember that the Coriolis force depends, in part, on latitude; its magnitude is relatively small at low latitudes and relatively large at high latitudes. Select the latitude where you want the action to take place by moving the marker up (higher latitude and larger Coriolis force) or down (lower latitude and smaller Coriolis force). With both the pressure-gradient force and the Coriolis force acting on the parcel, you can see that the forces exactly balance each other, and the air parcel now moves parallel to the isobars with low pressure to the left of the direction of motion (again, we're assuming we're in the Northern Hemisphere).
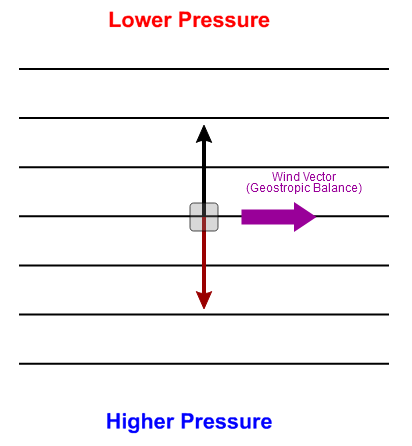
This balance between the pressure-gradient force and the Coriolis force is called geostrophic balance, and the wind that results is called the geostrophic wind. But, how does geostrophic balance develop? I won't focus on the details, the process goes something like this:
- As the air parcel accelerates in response to the pressure-gradient force, the magnitude of the Coriolis force also steadily increases because the magnitude of the Coriolis force increases as speed increases.
- As a result, deflections to the right become greater with time, with the Coriolis force acting 90 degrees to the right of the (continually changing) direction of motion.
- The parcel curves toward the right until the magnitude of the Coriolis force balances the pressure-gradient force (geostrophic balance), and the parcel moves parallel to the isobars with lower pressure on the left of the direction of motion. This state of geostrophic balance is what's depicted on the interactive force diagram (and shown on the right).
The atmosphere is constantly striving for balance, and in geostrophic balance, there is no net force acting on the air parcel (because the pressure-gradient force and Coriolis force balance each other). Therefore, (according to Newton's laws of motion) the parcel will cease its acceleration and continue to move in a fixed direction at a constant speed. In this case, the final direction of the air parcel is directly eastward (in other words, the wind blows from the west), but in general, the geostrophic wind blows parallel to local isobars. Regardless of the strength of the pressure-gradient force (you can try varying it in the interactive force diagram), the end result is geostrophic balance, with a stronger pressure-gradient force leading to faster wind speeds.
I should point out, however, that the geostrophic wind is an idealized wind. It never perfectly occurs in nature. As you know, near the surface of the earth, friction is a factor (which we're about to get into) that disrupts geostrophic balance. However, the real atmosphere is often very close to geostrophic balance at high altitudes, where friction becomes negligible. So, we could look at isobars on an upper-air weather map and immediately get an idea of the wind direction by always remembering that the geostrophic wind blows parallel to the isobars. Knowing that narrows down the possibilities for wind direction to essentially two choices. But, if you imagine standing on the map with the geostrophic wind at your back, low pressure should be on your left in the Northern Hemisphere, which will allow you to find the correct wind direction.
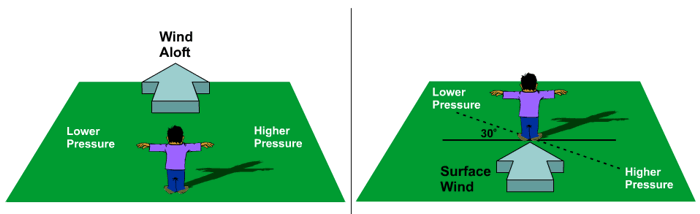
Near the surface, however, we have to deal with friction, so let's add it on the interactive force diagram. Make sure that the pressure gradient, Coriolis, and frictional forces are all turned on so that we can simulate real conditions on a surface weather map and observe the magnitude and the direction of the surface wind. Notice that the wind velocity vector got smaller (because friction slowed the wind speed) and now the wind blows across isobars in toward lower pressure somewhat. If you imagine standing with the surface wind at your back in the Northern Hemisphere, low pressure is still on your left, but on average, it will lie about 30 degrees clockwise from your left arm (as shown above on the right). By the way, these "rules" are known in meteorology as Buys Ballot's Law.
Even with friction in the mix, the forces still achieve balance. Again, I'm going to skip some of the details of how the balance is achieved, but the process basically works like this:
- friction acts to slow a moving air parcel, which reduces the velocity
- with the parcel moving slower, the magnitude of the Coriolis force is also reduced a bit
- with the Coriolis force a bit weaker than it was in a geostrophic case, the pressure-gradient force is a bit stronger than the Coriolis force, which pushes air parcels across local isobars in toward lower pressure (alternatively, away from higher pressure).
So, ultimately, both friction and the Coriolis force work to oppose the effects of the pressure gradient force, but eventually a balance develops between the three forces and the parcel moves at a constant direction and speed. The bottom line is that the final path of the parcel takes it across the isobars inward toward lower pressure and away from higher pressure.
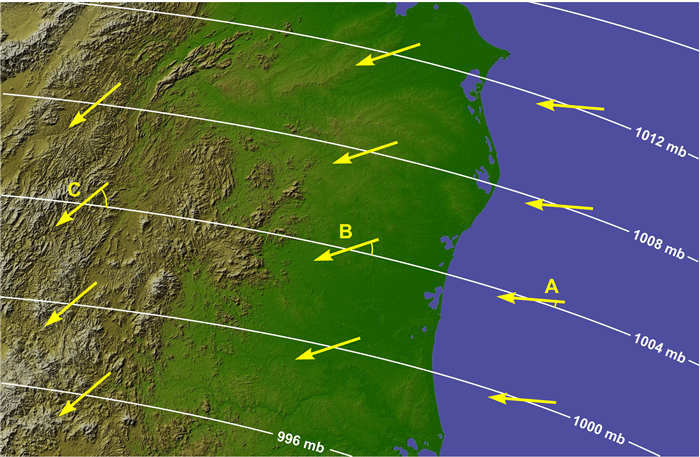
The angle at which a parcel crosses local isobars is determined largely by the magnitude of friction, and as you'll recall, friction depends on the velocity of the parcel as well as the roughness of the surface. Over land, the wind crosses the isobars at approximately 30 degrees, on average. Over the ocean and Great Lakes, the crossing angle (the angle at which the wind crosses the isobars) is generally less than 30 degrees, owing to less friction over usually smoother water (compared to rough land). Essentially, with less friction, the wind over the water is a bit closer to geostrophic than it is over land. In mountainous areas, where the effects of friction are greater, the crossing angle can be 45 degrees or even more. The difference in crossing angles can frequently be seen on weather maps (like the idealized map below).
It's the combination of the forces you've learned about that give rise to the counterclockwise flow around areas of low pressure (and clockwise flow around areas of high pressure) that you've seen on surface weather maps, like the sea-level pressure analysis from 18Z on September 8, 2011 that I showed previously. In order to help you visualize the movement of air on maps of sea-level pressure, I created a couple of short videos that I think will help summarize the concepts we've covered, and help you determine wind direction from a map of isobars. The first video (1:46) will help you see how air parcels move depending on which forces are acting on them.
Let’s examine that paths air parcels will follow on this idealized weather map, based on the combination of forces acting on the parcels.
We have a map of sea-level pressure here, with an area of low pressure marked and an area of high pressure marked.
For our first case, we’ll pretend that only the pressure gradient force is acting on air parcels, which are marked by these purple boxes. If only the pressure gradient force acts, air parcels cross isobars perpendicularly, flowing from higher pressure toward lower pressure, like this
Now, let’s add in the Coriolis force. If only the pressure-gradient force and the Coriolis force act on air parcels, they’re in a state of geostrophic balance, and the Coriolis force turns the air parcels 90 degrees to the right of the original direction of motion in the Northern Hemisphere. So, air parcels in geostrophic balance flow parallel to local isobars, with lower pressure on the left of the direction of motion. You can also see the general counterclockwise flow around the low pressure, and the clockwise flow that results around highs.
Now, let’s add in friction, for the most realistic look at how air really flows near Earth’s surface. Friction disrupts geostrophic balance by slowing down the air parcels, which weakens the Coriolis force slightly. Eventually a balance develops between the pressure-gradient force, the Coriolis force, and friction, with parcels now crossing local isobars in toward lower pressure as they flow counterclockwise around lows and clockwise around highs.
To see the process of determining wind direction on a real map of sea-level isobars, check out the short video (3:09) below, in which I walk through a "recipe" for determining wind direction.
One of the objectives from the lesson, and a really useful skill, is to be able to look at a map of isobars and estimate the wind direction at any given point. And using the concepts from the lesson, we can do that. So I'm going to walk you through, kind of, the recipe that I go through when I need to estimate wind direction at a given point.
The first thing we have to do is we have to pretend that we're dealing with geostrophic winds. Now, with the geostrophic wind, we know that the pressure gradient force is exactly balanced by the Coriolis force. But in practical terms, the important thing about geostrophic winds is that they blow parallel to local isobars.
So at point A here, if we have winds blowing parallel to local isobars, they're either going to be from the southwest, or from the northeast. There's only two choices. So we have to determine which way they'd be blowing from.
And to do that, we have to remember our circulations around areas of high and low pressure. In the Northern Hemisphere, we have counterclockwise circulation around areas of low pressure, so that's going to give us a general sense of the wind flow that's like this. And that means that we have geostrophic winds that would be blowing from the southwest at point A.
Another way to think about it is that if you're standing with the wind at your back, lower pressures are going to be on your left. So if we stood with our wind at our backs at point A, and we were looking off toward the northeast, the only thing that makes sense is a southwesterly wind because that gives us lower pressures on our left. So geostrophic winds would be from the southwest, blowing parallel to local isobars at point A.
But we have to account for friction. The wind actually isn't geostrophic. Friction throws off the balance between the pressure gradient force and the Coriolis force, and it slows the wind down. But it also changes its direction and causes it to cross local isobars in toward lower pressure at a 30-degree angle, on average.
So if we take that into account, that means that the winds are going to cross the local isobars in toward lower pressure, about a 30-degree angle. And that's going to give us a wind that's almost from due south. Something around 180 degrees, give or take a little bit. So that's going to be our approximate wind direction at point A when we've accounted for friction as well.
We can do a similar analysis at point B. If we first pretend that the winds are geostrophic at point B, they're parallel to local isobars. So they're either from the east-northeast or from the west-southwest. And to figure out which one it is, we remember that air circulates clockwise around areas of high pressure in the Northern Hemisphere. So our general flow is going to be clockwise like this, and our wind flow is going to be from the east-northeast, parallel to these isobars. The geostrophic winds are going to be parallel to those isobars from the east-northeast.
But we have to account for friction, too. And to do that, we have to cross isobars at about a 30-degree angle away from higher pressure. So our winds would look something more like this, and ours winds would be from the northeast, or even north-northeast, at probably something like 20 or 30 degrees when we've accounted for friction because we don't actually have geostrophic winds.
Using the recipe described in the video above, you should be able to estimate the wind direction just about anywhere on a map of isobars, but I think it's important that you get some practice. Therefore, I've dedicated the next section to an activity that will help you refine this Key Skill. Read on!