Prioritize...
When you've completed this section, you should be able to describe the three main sources of error in computer model forecasts described in this section (initialization errors, computational errors, and oversimplifications / parameterizations).
Read...
There's no doubt that computers have helped revolutionize weather forecasting, making weather forecasts for anywhere in the world easily accessible and reasonably accurate several days into the future (most of the time). But, for all of the wonders of computer models, their forecasts always contain errors. Remember the quote from British statistician George Box that I mentioned when we discussed general circulation models: "All models are wrong, but some are useful." Well, that idea applies here, too. Indeed, a big part of a weather forecaster's job today is analyzing model forecast data to determine which parts will be useful in making a forecast.
A number of sources of error are present in all computer model forecasts. In this section, I'll focus on three of the biggest sources: errors in the model's initialization, computation errors (errors resulting from the way computers perform calculations), and oversimplifications of some atmospheric processes in the model. Let's start at the beginning, with the model's initialization.
Initialization Errors
In order to create a perfect short-term weather forecast, a computer model would need a perfect representation of the initial state of the atmosphere. In other words, we would need to precisely and accurately measure all relevant atmospheric variables (temperature, dew point, pressure, wind speed and direction, precipitation-rate, etc.) continuously at every single point in the atmosphere. Can we do that? Not even close! And, such perfect and continuous measurements aren't going to happen in the foreseeable future, either.
So, we can't perfectly measure the atmosphere everywhere all the time. That's not surprising, but guess what: The observations we do have aren't perfect, either. Yes, occasionally instruments that measure things like pressure, temperature, and wind speed go awry and take erroneous measurements. This instrumental error is unavoidable, and while meteorologists try to identify and weed out the bad data, catching all of it is practically impossible. So, a little "observational error" sneaks its way into the model's initialization.
Another type of observational error arises from the way observational data are spatially distributed. It turns out that to best solve the equations that predict the future state of the atmosphere, data need to be organized in some evenly spaced manner. Furthermore, the more closely spaced the data, the better. Now take a look at the distribution of official surface observing stations in Europe and parts of Asia (below). Notice the erratic distribution of stations -- some are tightly clustered together, while huge gaps exist between others. But, before a weather model can be run, it needs a more even distribution of data.
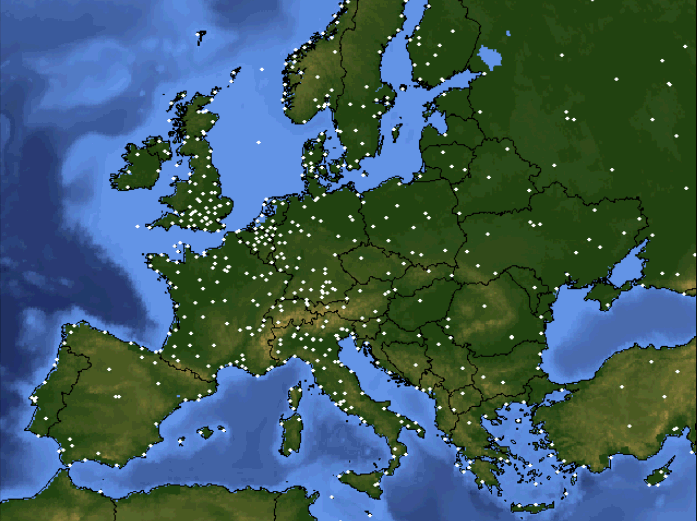
A more even distribution of data can be achieved through a mathematical form of estimation called interpolation, but the estimates are imperfect. For example, consider a case where we have two observing stations located 100 miles apart, with temperatures of 50 degrees Fahrenheit and 40 degrees Fahrenheit, respectively. The computer model, however, needs to know the temperature at a point located exactly between the two observation stations. What temperature should it use? 45 degrees Fahrenheit seems like a reasonable guess, but is it right? Well, unless we have an actual measurement from that location, we don't know for sure (and neither does the computer model). While sophisticated approaches for manipulating irregularly spaced data exist, they're all imperfect, and all cause small errors to creep into the model's initialization.
Of course, a computer model must simulate the atmosphere in three dimensions, so it needs initialization data for conditions above the surface of the Earth, too. Weather balloon launches, which typically occur twice each day around the world at 00Z and 12Z, help provide some of that data. However, primarily due to the materials costs associated with launching sensors by balloon into the atmosphere every day, there are relatively few upper-air observing sites where weather balloons are launched. For example, here's a map of the upper-air observing sites in North America. In the U.S., there's usually only a few in each state, at best, and large gaps exist in between observation sites. Some models incorporate observations taken aboard aircraft into their initializations in an effort to increase the number of upper-air observations in the model initialization.
Still, gaps exist, and measurements from satellites help fill in the gaps of the upper-air observing network. While satellite data have greatly helped improve model initialization quality, the remotely sensed observations from satellites still aren't perfect and are another source of error in the initialization. Regardless of the flaws, all of these observations, along with the model's forecast from the previous run (which, itself, is imperfect) are woven together using complex mathematical schemes to create the initialization, which serves as the starting point where the computer begins calculating changes to atmospheric variables in the future.
But, just what is the effect of imperfections in the model's initialization on the forecast? In "chaotic" systems like the atmosphere, imperfections in the initialization are a big deal. Perhaps you've heard of "chaos theory" before. Chaos theory essentially boils down to the idea that any changes in the initial conditions of the atmosphere can cause the system to evolve differently.
In popular culture, the phrase "butterfly effect" is often used as a metaphor for chaos theory (here's a mildly amusing cartoon linking the butterfly effect to weather). The metaphor suggests that a seemingly random flapping of a butterfly's wings in Brazil (or wherever) could eventually affect weather on a larger scale. In reality, this idea is pretty silly. Any flap of a butterfly's wings in Brazil would be dampened out locally by other larger-scale forces, and thus there's no way that a butterfly could alter the weather a month later in some distant part of the world. Perhaps an armada of millions of butterflies flapping their wings for an hour could have an effect, but not one measly butterfly. Still, imperfections in computer-model initializations do matter, because the errors can rapidly grow, paving the way for wildly inaccurate predictions and vastly different forecasts each time the model runs. For a visual on what I mean, check out the short video below (2:16), which is based on a simulation using equations developed by a pioneer of chaos theory, Edward Lorenz.
Video: Growing Errors in Computer Model Weather Forecasts (2:16)
I’m going to use a simulation to help you visualize how errors can grow in a computer model weather forecast. This graph will actually show two model simulations, one with a blue trace and one with a red trace. The simulations are based on the same model, with one key difference – the initialization.
We’ll pretend that Simulation 1, which will be marked by a blue trace, has a perfect initialization, which in real life is actually impossible because we can’t perfectly measure the atmosphere everywhere at all times. Meanwhile, Simulation 2, which will be marked by a red trace, has a small error in its initialization of just .01%.
These simulations are based on the Lorenz Equations that describe chaotic systems like the atmosphere, and we’ll imagine that our simulations are predictions of atmospheric vertical motion. Computer models have to predict vertical motion in order to predict things like cloud formation and precipitation.
We see the simulations’ predictions for vertical motion are basically identical initially, with perhaps some very small differences where you can pick out the difference between the blue and red traces from time to time, but overall there’s near perfect agreement. As time goes on, let’s see what happens…
…eventually the disagreement grows larger until the solutions become wildly different.
Now let’s see what happens when the initialization error in Simulation 2 is a bit larger – 1% this time. We’ll start the simulations and we see that there’s near perfect agreement initially again. But, we start to see bigger differences in the solutions faster this time, and the solutions very quickly bear no resemblance to each other.
And so it is in computer models that predict the weather. Errors in the computer model’s initialization grow in time. The errors tend to be small at first, but as they grow larger, eventually the model’s forecast bears little resemblance to what will actually happen with the weather.
Note that even small errors in the model's initialization (one percent or less!) create simulations that are vastly different eventually. The larger the error in the initialization, the faster the solutions diverge. The bottom line is that the errors from the model's initialization grow in time, and the larger the error in the initialization, the faster the errors in the model forecast tend to grow.
Computational Errors
But, computer-model errors don't stop with the initialization. Other errors get introduced into computer-model forecasts within the calculations themselves. For starters, rounding numbers can introduce error (even rounding 59.9999 degrees Fahrenheit to 60 degrees Fahrenheit can make a difference). Also, each calculation is performed for some "time step" into the future (maybe a minute or two), and then the values calculated for that time are used as the basis for calculations another virtual minute or two into the future. But, skipping calculations for the times in between each "time step" also introduces errors. These errors could be reduced by making the model's time step shorter (leaving less time between the calculations), but that requires more computing power. Furthermore, computer models perform their calculations only at certain spots on the virtual Earth, and then interpolate the results to cover the whole globe, further introducing error. Again, this error could be reduced by performing the calculations at more sites that are closer together, but doing so requires more computing speed and power.
Oversimplifications (Parameterizations)
Finally, some processes are oversimplified in the model because of their immense complexity. The details of radiation budgets and turbulent air motions near the ground, along with atmospheric convection (in some models) are so complex that we cannot model them accurately. Just think of the complexity of the surface of the Earth, for example, with parking lots, agricultural fields, forests, buildings, mountains, etc. Each nuance affects the local radiation budget and the way air moves over the ground (and humans can change the landscape with urban development). So, very small-scale atmospheric processes like radiation budgets near the ground tend to be "parameterized" in the models. Formally, a parameterization is an oversimplified way to simulate a process. Of course, since parameterizations imperfectly simulate atmospheric processes, they introduce more errors into the model forecast, which tend to grow in time.
After hearing about how erroneous model forecasts can be, it might be tempting to think that model forecasts are useless. But, even though they're wrong, experienced weather forecasters who know the strengths and limitations of computer models find them very useful in making weather forecasts. Given their imperfect nature (flawed initializations and oversimplifications) meteorologists don't just run one computer model. Instead, they run many computer models! Using an "ensemble" of computer models helps meteorologists better understand the range of possibilities in the forecast, and we'll cover these so-called "ensemble forecasts" next!