The Four Laws of Radiation

Read...

In order to best make use of the of information that comes to us via the electromagnetic spectrum, we need to understand some basic properties of radiation. A complete treatment on the subject of radiation theory would take an entire course at least (indeed, folks pursuing a degree in meteorology are usually required to take a Radiative Transfer course). Instead, you just need to know the fundamental principles describing the electromagnetic radiation that originates from an object, and how that radiation travels through space (which we'll get into soon).

For electromagnetic radiation, there are four "laws" that describe the type and amount of energy being emitted by an object. In science, a law is used to describe a body of observations. At the time the law is established, no exceptions have been found that contradict it. The difference between a law and a theory is that a law simply describes something, while a theory tries to explain "why" something occurs. As you read through the laws below, think about observations you've made in everyday life that might support the existence of each law.

Planck's Law

Planck's Law can be generalized this way:  Every object emits radiation at all times and at all wavelengths. Does that surprise you? We know that the sun emits visible light (below left), infrared waves, and ultraviolet waves (below right), but did you know that the sun also emits microwaves, radio waves, and X-rays? Of course, the sun is a big nuclear furnace, so it makes sense that it emits all sorts of electromagnetic radiation. However, Planck's Law states that every object emits over the entire electromagnetic spectrum. That means that you emit radiation at all wavelengths, and so does everything around you!

Two images of the sun taken at different wavelengths of the electromagnetic spectrum. The left image shows the sun's emission at a wavelength in the visible range. The right image is the ultraviolet emission of the sun. Note: colors in these images and the ones above are deceptive. There is no sense of "color" in spectral regions other than visible light. The use of color in these "false-color" images is only used as an aid to show radiation intensity at one particular wavelength.

Credit: NASA/JPL

Now before you dismiss this statement out-of-hand, let me say that you are not emitting X-rays in any measurable amount. The mathematics behind Planck's Law hinge on the fact that there is a wide distribution of vibration speeds for the molecules in a substance. This means that it is possible for matter to emit radiation at any wavelength, and in fact it does, but the amount X-rays you're currently emitting, for example, is unimaginably small.

Another common misconception that Planck's Law dispels is that matter selectively emits radiation. Consider what happens when you turn off a light bulb. Is it still emitting radiation? You might be tempted to say "No" because the light is off. However, Planck's Law tells us that while the light bulb may no longer be emitting radiation that we can see, it is still emitting at all wavelengths (most likely, it is emitting copious amounts of infrared radiation). Another example that you hear occasionally on TV weather casts goes something like this: "When the sun sets, the ground begins to emit infrared radiation..." That's just not how it works. The ground doesn't "start" emitting when the sun sets. Planck's Law tells us that the ground is always emitting infrared radiation, a fact that we'll explore later on in this lesson.

Wien's Law

So, Planck's Law tells us that all matter emits radiation at all wavelengths all the time, but there's a catch: Matter does not emit radiation at all wavelengths equally. This is where the next radiation law comes in. Wien's Law states that the wavelength of peak emission is inversely proportional to the temperature of the emitting object. Put another way, the hotter the object, the shorter the wavelength of maximum emission. You have probably observed this law in action all the time without even realizing it. Want to know what I mean?  Check out this steel bar. Which end might you pick up? Certainly not the right end! It looks hot, doesn't it? Why does it "look hot?"

Well, for starters, the peak emission for the steel bar (even the part that looks really hot) is in the infrared part of the spectrum. But, the right side of the bar is hotter than the left, and therefore the right side has a shorter wavelength of peak emission compared to the left side. You see this shift in the peak emission wavelength as a color change from red to orange to yellow as the metal's temperature increases. In fact, the right side is hot enough that its peak emission is pretty close to the visible part of the spectrum (which has shorter wavelengths than infrared); therefore, a significant amount of visible light is also being emitted from the steel.

Judging by the look of this photograph, the steel has a temperature of roughly 1500 kelvins, resulting in a max emission wavelength of 2 microns (visible light has wavelengths of 0.4-0.7 microns). Here is a chart showing how I estimated the steel temperature. To the left of the visibly red metal, the bar is still likely several hundred degrees Celsius. However, in this section of the bar, the peak emission wavelength is far into the infrared portion of the spectrum, and no visible light emission is discernible with the human eye.

So, how do we apply Wien's Law to the emission sources that effect the atmosphere? Consider the chart below showing the emission curves (called Planck functions) for both the sun and the earth.

The emission spectrum of the sun (orange curve) compared to the earth's emission (dark red curve). The x-axis shows wavelength in factors of 10 (called a "log scale"). The y-axis is the amount of energy per unit area per unit time per unit wavelength. I have kept the units arbitrary because they are quite messy. The important message is that the sun's emission spectrum peaks in the visible spectrum while the earth's emission spectrum peaks in the infrared (because of Wien's Law).

Credit: David Babb

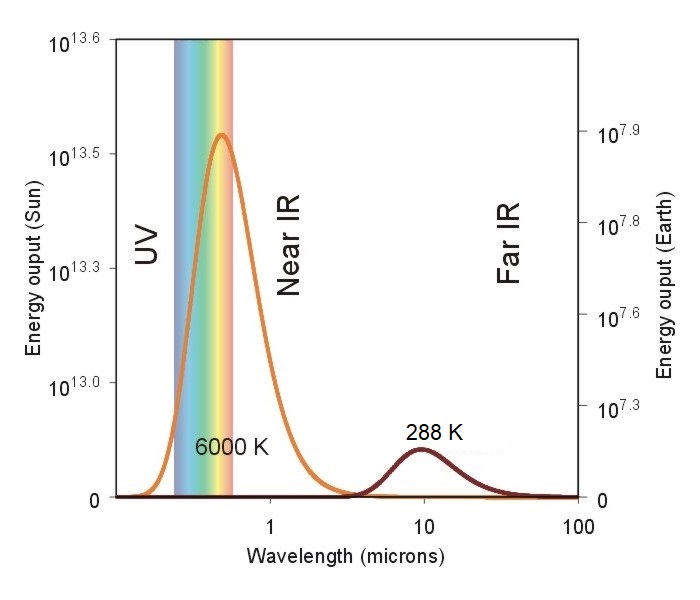
Note the idealized spectrum for the earth's emission of electromagnetic radiation (dark red line) compared to the sun's electromagnetic spectrum (orange line). The radiating temperature of the sun is 6000 degrees Celsius compared to the earth's measly 15 degrees Celsius. This means that given its high radiating temperature, the sun's peak emission occurs in the visible light portion of the spectrum, near 0.5 microns (toward the short-wave end of the EM spectrum). That wavelength is also the reason why we see the sun as having a yellow hue. Meanwhile, the earth's peak emission is located in the infrared portion of the electromagnetic spectrum (having longer wavelengths, by comparison).

Stefan–Boltzmann Law

Look again at the graph of the sun's emission curve versus the earth's emission curve (above), and take note of the energy values on the left axis (for the sun) and right axis (for the earth). The first thing to notice is that the energy values are given in powers of 10 (that is, 10⁶ is equal to 1,000,000). This means that if we compare the peak emissions from the earth and sun we see that the sun at its peak wavelength emits nearly 3,000,000 times more energy than the earth at its peak. In fact, if we add up the total energy emitted by each body (by adding the energy contribution at each wavelength), the sun emits over 180,000 times more energy per unit area than the earth! 

I calculated the number above using the third radiation law that you need to know, the Stefan-Boltzmann Law. The Stefan-Boltzmann Law states that the total amount of energy per unit area emitted by an object is proportional to the 4th power of the temperature. You won't need to do any specific calculations with the Stefan-Boltzmann Law, but you should understand that as temperature increases, so does the total amount of energy per unit area emitted by an object (hotter objects emit more total energy per unit area than colder objects). This relationship is particularly useful when we want to understand how much energy the earth's surface emits in the form of infrared radiation. It will also come in handy when we study the interpretation of satellite observations of the earth, later on.

Kirchhoff's Law

In the preceding radiation laws, we have been talking about the ideal amount of radiation that can be emitted by an object. This theoretical limit is called "black body radiation." However, the actual radiation emitted by an object can be much less than the ideal, especially at certain wavelengths. Kirchhoff's Law describes the linkage between an object's ability to emit at a particular wavelength with its ability to absorb ("take in") radiation at that same wavelength. In plain language, Kirchhoff's Law states that for an object with constant temperature, an object that absorbs radiation efficiently at a particular wavelength will also emit radiation efficiently at that wavelength. Kirchoff's Law has lots of consequences for how we observe weather from space using satellites (a topic we'll revisit later).

Now that we've covered the basic behavior of radiation and how it relates to temperature, we need to wrap-up our look at radiation by examining at the possible fates of  "beam" of radiation as it passes through a medium.