Heat Capacity and Energy Storage
When our planet absorbs and emits energy, the temperature changes, and the relationship between energy change and temperature change of a material is wrapped up in the concept of heat capacity, sometimes called specific heat. Simply put, the heat capacity expresses how much energy you need to change the temperature of a given mass. Let’s say we have a chunk of rock that weighs one kilogram, and the rock has a heat capacity of 2000 Joules per kilogram per °C — this means that we would have to add 2000 Joules of energy to increase the temperature of the rock by 1 °C. If our rock had a mass of 10 kg, we’d need 20,000 Joules to get the same temperature increase. In contrast, water has a heat capacity of 4184 Joules per kg per °K, so you’d need twice as much energy to change its temperature by the same amount as the rock.
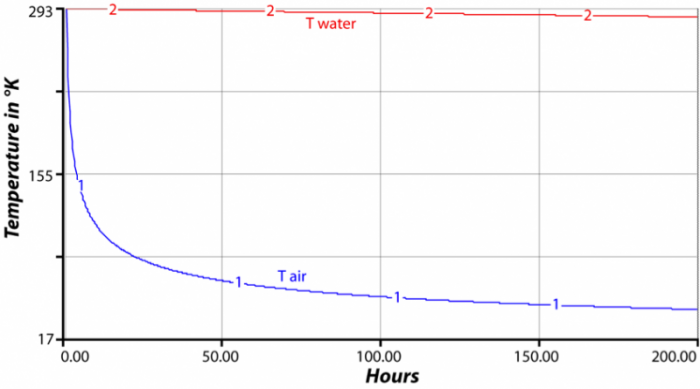
This image is a line graph showing the cooling of air temperature over time in comparison to a constant water temperature. The graph plots temperature in Kelvin against time in hours, illustrating the cooling process of air.
- Graph Type: Line graph
- Y-Axis: Temperature (K)
- Range: 17 K to 293 K
- X-Axis: Hours
- Range: 0 to 200 hours
- Data Representation:
- Water Temperature (T_water): Red line
- Constant at 293 K (labeled as 2) throughout the 200 hours
- Air Temperature (T_air): Blue line
- Starts at 155 K (labeled as 1) at 0 hours
- Decreases rapidly within the first 50 hours, approaching 17 K
- Levels off near 17 K after 100 hours, remaining stable through 200 hours
- Water Temperature (T_water): Red line
- Trend:
- Air temperature cools significantly from 155 K to near 17 K within the first 100 hours
- Water temperature remains unchanged at 293 K
The graph demonstrates the rapid cooling of air over time while the water temperature remains constant, highlighting the difference in thermal behavior between air and water over a 200-hour period.
The heat capacity of a material, along with its total mass and its temperature, tell us how much thermal energy is stored in a material. For instance, if we have a square tub full of water one meter deep and one meter on the sides, then we have one cubic meter of water. Since the density of water is 1000 kg/m3, this tub has a mass of 1000 kg. If the temperature of the water is 20 °C (293 °K), then we multiply the mass (1000) times the heat capacity (4184) times the temperature (293) in °K to find that our cubic meter of water has 1.22e9 (1.2 billion) Joules of energy. Consider for a moment two side-by-side cubic meters of material — one cube is water, the other air. Air has a heat capacity of about 1000 Joules per kg per °K and a density of just 1.2 kg/m3, so its initial energy would be 1000 x 1 x 1.2 x 293 = 351,600 Joules — a tiny fraction of the thermal energy stored in the water. If the two cubes are at the same temperature, they will radiate the same amount of energy from their surfaces, according to the Stefan-Boltzmann law described above. If the energy lost in an interval of time is the same, the temperature of the cube of air will decrease much more than the water, and so in the next interval of time, the water will radiate more energy than the air, yet the air will have cooled even more, so it will radiate less energy. The result is that the temperature of the water cube is much more stable than the air — the water changes much more slowly; it holds onto its temperature longer. The figure above shows the results of a computer model that tracks the temperature of these two cubes.
One way to summarize this is to say that the higher the heat capacity, the greater the thermal inertia, which means that it is harder to get the temperature to change. This concept is an important one since Earth is composed of materials with very different heat capacities — water, air, and rock; they respond to heating and cooling quite differently.
The heat capacities for some common materials are given in the table below.
| Substance | Heat Capacity (Jkg-1K-1) |
|---|---|
| Water | 4184 |
| Ice | 2008 |
| Average Rock | 2000 |
| Wet Sand (20% water) | 1500 |
| Snow | 878 |
| Dry Sand | 840 |
| Vegetated Land | 830 |
| Air | 1000 |
