Lab 3: Climate Modeling

Lab 3: Climate Modeling Instructions

Once you are done answering the questions below, enter your answers into the Module 3 Lab Submission (Practice) to check your answers. If you didn’t do as well as you'd hoped, review the course materials, including the instructional videos, or post questions to the Yammer group to ask for clarification of a particular topic or concept. After that, open the Module 3 Lab Submission (Graded) and complete the graded version of the lab. The graded lab mostly includes questions similar to the practice lab, but has some additional questions.

Download this lab as a Word document: Lab 3: Climate Modeling (Please download required files below.)

Use this Model for Questions 1 - 4. Please Note: The model in the videos below may look slightly different than the model linked here. Both models, however, function the same.

Video: The Simplest Climate Model (Questions 1-3) Part 1 (3:21) 

Video: The Simplest Climate Model (Questions 1-3) Part 2 (2:38)

Changing Initial Temperature

1. How will changing the initial temperature affect the model? We saw that when we started with an initial temperature (remember that this is the global average temp.) of 0°, the model ended up with a temperature of about -18°C. What will happen if we start with a different initial temperature? Change the initial temperature to 1, then run the model and take note of the ending temperature by placing your cursor over the curve at the right-hand side (where the time is 30 years) and then click and you should see the little box that tells you the position of your cursor. You should round this temperature to the nearest whole number. Select your answer from the following:

   A. 10°

   B. -8°C

   C. -18°C

   D. -33°C

   Click on the Restore all Devices button when you are done, before going on to the next question.

   Changing the Albedo

2. What will happen to our climate model if we change the albedo? Recall that a low albedo represents a dark-colored planet that absorbs lots of solar energy, while a higher albedo (it can only go up to 1.0) represents a light-colored planet that reflects lots of solar energy. Change the albedo to 0.5, then run the model and find the ending temperature, and select your answer from the following:

   A. about -38(plus or minus 1)

   B. about 2 (plus or minus 1)

   C. about -1 (plus or minus 1)

   D. about -16 (plus or minus 1)

   Click on the Restore all Devices button when you are done, before going on to the next question.

   Changing the Emissivity

3. Next, we will see what happens when we change the emissivity. Recall that if the emissivity is 1.0, the planet has no greenhouse effect and as the emissivity gets smaller, it represents a stronger greenhouse effect — so, how will this change our climate model? Change the emissivity to 0.3, then run the model and find the ending temperature, and select your answer from the following:

   A. about -18 (plus or minus 1)

   B. about 47 (plus or minus 1)

   C. about 16 (plus or minus 1)

   D. about 71 (plus or minus 1)

   Click on the Restore all Devices button when you are done, before going on to the next question.

   Changing the Solar Constant

   Video: The Simplest Climate Model (Question 4) (3:24)

   Click here for a transcript of The Simplest Climate Model video.

   For problem number four, we're gonna see what happens to the climate model in response to a brief change in the solar constant. We’re gonna increase the solar constant for a little bit and see how the model reacts. But before doing that, we're going to try to set the model up, to begin with, in such a way that it represents something like our earth. So, we're going to change the emissivity first to .61, that's an emissivity value that kind of represents the strength of our greenhouse. We're going to change the initial temperature of our planet to 15 and we'll leave the other things the same. Then we're going to go to the solar constant here and click on that. And right here in the middle of this graph, I'm going to position the cursor right here and click one little tick mark up. There, so I've made a graph now of the solar constant so that it's steady at 1370, then it bumps up to 1372 here for a little bit, and then it drops back down like that to 1370 for the rest of the time. You hit okay, and now we're ready to run the model to see what happens. So, it's evaluating it and we're about to see the results here. So, we see in magenta now the temperature of our climate model is staying constant at 15, up until the point where the solar constant starts to increase. And then, as it increases, the planetary temperature increases to 15.05, it peaks there. And notice that that peak occurs at 16.6 years, 16.7 years, something like. That's about 1.7 years after the peak in the solar constant value. So, that's what we call a lag time, a difference in time between the peak of some kind of forcing (like the solar constant) and the response, which is the planetary temperature. So, it peaks at about 1.7, 1.8 years later. And then it drops back down. It doesn't quite get back down to 15 after we have restored the solar constant to 1370, because the system takes a while to sort of settle down again and that's a function of the kind of thermal mass of the climate system, which is related to the ocean temperature. And so, what we're going to do in this in this question, is to change the ocean depth from its default value of 100 to different values, by simply typing in a different value here. So, there's 200, and then running the model and comparing the response of the model to this kind of control version here that we're looking at in this little video. So you might want to, in fact, you should, take note of the maximum temperature rise of the model, following this spike in the solar constant, and the timing of that as well.

   Credit: Dutton

   The solar constant is not really constant for any length of time. For instance, it was only 70% as bright early in Earth’s history, and it undergoes smaller, more rapid fluctuations (and much smaller) in association with the 11-year sunspot cycle. Let’s see how the temperature of the planet reacts to changes in the solar constant. First, we need to run a “control” version of our model, as is shown in the video above. Set the model up with the following parameters:

   Initial Temp = 15°C

   Albedo = 0.3

   Emissivity = 0.6147 (enter the value manually in the box)

   Ocean Depth = 100 m

   Solar Constant — alter graph as shown in the video. Note the lines in the Solar Constant graph do not line up exactly with numbers. To get the exact number (1372) click on the Solar Constant Plot, then on Graph and enter the value at X=15 Y-1372.

   Record the peak temperature (should be 15.04 deg C) and the time lag (should be 1.7 years).

4. What we are going to look at now is how the ocean depth affects the way the model responds to this spike in the solar constant. In our control, the ocean depth is 100 m — this means that only the upper 100 m of the oceans are involved in exchanging heat with the atmosphere on a timescale of a few decades. If the oceans were mixing faster, this depth would be greater, and if they were mixing more slowly, the depth would be less. Change the ocean depth to 50 m. Then run the model and note the peak value of the temperature and estimate the lag time, for comparison with the control version. Select your answer from the following:

   A. Peak temp > control; lag time > control

   B. Peak temp < control; lag time > control

   C. Peak temp > control; lag time < control

   D. Peak temp < control; lag time < control

   Adding a Feedback

   Use this Model for Question 5. Please Note: The model in the videos below may look slightly different than the model linked here. Both models, however, function the same.

   Now, we’re ready to try something more challenging and more realistic. In the real world, the surface temperature has a big impact on the albedo — when it gets very cold, snow and ice will form and increase the albedo. So, there is a feedback in the system — a temperature change will cause an albedo change, which will cause a temperature change, and so forth. To explore this feedback, we need to work with an altered version of the model, where we have defined the relationship between albedo and temperature as follows:

   

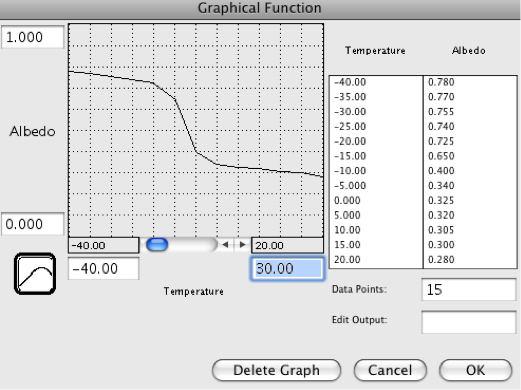   Relationship between albedo and temperature in the revised model

   Credit: David Bice © Penn State University is licensed under CC BY-NC-SA 4.0

   This graph implies that there is a kind of threshold temperature of about -10 to -15°C, at which point the whole planet becomes frozen. The suggestion is that even with a very cold global temperature of 0 °C, the equatorial region might be relatively ice-free and would thus have a low albedo, but as the temperature gets colder, even the tropics become covered by snow and ice. Once that happens, the planetary albedo changes only slightly. Likewise, at higher temperatures, the albedo decreases only slightly since there is so little snow and ice to remove.

   This important to understand what this model includes — a link between planetary temperature and planetary albedo. As the temperature changes, so the albedo changes, and as the albedo changes, so the insolation changes, and as the insolation changes, so the temperature changes — this is a feedback mechanism. Feedback mechanisms are very important components of many systems, and our climate system is full of them.

   Video: Simple Planetary Climate Model (Question 5) (4:20)

   Click here for the Simple Planetary Climate Model (Question 5) video.

   For problem number five, we have a slightly different model of the climate system that's got a few new features to it. We see the initial temperature and albedo and ocean depth from before. The solar multiplier here is just something that, if it's one, it's not going to change the solar input at all. If I make that greater, like 2 or 1.5 or 3, or something, that's going to increase, it's going to multiply solar constant by 1.3 in this case. I'm going to do that here. It also has something called a CO2 multiplier and it does the same thing to the CO2 concentration. So, here it is set at 1 initially. I could make that 2 and then in that case instead of having 380 parts per million CO2, we'd have 760. So, we would double it. And if I made this be 0.5 then we would cut our CO2 concentration in half, and in doing that, we're changing the greenhouse effect of the climate model. We could change the history of atmospheric CO2 using this graph here, but we're not going to work with that in number five. It also has a couple of switches down here, one for a solar cycle and one for the albedo switch. And this albedo switch is the most important thing for this problem. When it's in this position, it's off. And then, we have just a constant albedo that's assigned up here in this box. But if we turn that thing on by going “click”, like that, it's suddenly now is going to make the albedo be a function of temperature, and that creates a feedback mechanism that does some interesting things. You'll kind of explore that in this problem. Let me just show you a few things here. So, if we restore everything to the way it was when you first opened the model and you just run it. You see that in page 1 of this graph pad, everything is just constant all the way across here. CO2, solar input, and temperature are staying the same. I'm going to switch to page 3 of this and this shows the temperature for the first run here. Now, if I switch the albedo switch on, I'm activating that feedback mechanism. But if I run it, it doesn't change anything at all. Okay, now watch this. I'm going to turn that back off. I'm going to decrease the CO2 multiplier. I'm going to make it be point something very small, point one, let’s say. Let's change that to point one, and now I'm going to run the model and see what happens. So, it gets quite a bit colder because we've taken a lot of CO2 out of that atmosphere here. It gets down to 8.3 at the end of eighty years. Now, if I turn the albedo switch on, see what happens now. Now, the temperature really drops. It drops to -5.6. So, the difference between -5.6 and this 8.3, that's the impact of the feedback mechanism. It has an effect, a cooling effect, from 8.3 to -5.6, so something more than 13 degrees of a negative shift in temperature for that feedback mechanism. So, in this problem, you're going to be assigned a CO2 multiplier value and you'll type that in here. It'll be something like 0.25 or 0.5 or 2 or 4 or something along those lines. You enter that number in there. Let's say you've got 4, and then you run the model with the albedo switch off and then you run it again with the albedo switch on, and you look at the temperature difference between those two runs of the model to get a sense of how big the albedo feedback effect is in our climate system.

   Credit: Dutton

   By definition, feedback mechanisms are triggered by a change in a system — if it is in steady state, the feedbacks may not do much. In the above graph, you may notice that at a temperature of 15°C (our steady state temperature), the albedo is 0.3, which is the albedo of our steady state model. So, if we run the model with an initial temperature of 15 °C, and an unchanging solar constant of 1370, our system will be in a steady state and we will not see the consequences of this feedback. But, if we impose a change on the system, things will happen.

   The change we will impose involves the greenhouse effect. The model includes something called the CO2 Multiplier. When this has a value of 1, it gives us a CO2 concentration of 380 ppm, which is the default value that gives us a temperature of 15°C. If we change it to 2, we then have 760 ppm and a stronger greenhouse, which leads to warming. If we change it to 0.5, we then have 190 ppm and a weaker greenhouse, thus cooling.

   You will be given a value for the CO2 Multiplier; enter that into the model and run it with the Albedo Switch in the off position (see the video) and note the ending temperature. Then turn the Albedo Switch on, which activates the feedback mechanism, and run the model again, noting the ending temperature. The difference between these two temperatures is what you need for your answer. For example, if you set the CO2 Multiplier to 3 and run the model with the Albedo Switch turned off, you see an ending temperature of 18.17°C, and then with the switch turned on, the ending temperature is 24.86°C, so the temperature difference due to the albedo feedback is +6.69°C — this is the answer you would select.

   Set the CO2 Multiplier to 6.0

5. What is the temperature difference due to the albedo feedback? Choose the answer that most closely matches your result. Be sure to study page 3 of the graph pad to get your results.

   A. about -5°C

   B. about +11°C

   C. about +18°C

   D. about -20°C

   Causes of Climate Change

   Use this Model for Questions 6-7. Please Note: The model in the videos below may look slightly different than the model linked here. Both models, however, function the same.

   Things that can cause the climate to change are sometimes called climate forcings. It is generally agreed upon that on relatively short time scales like the last 1000 years, there are 4 main forcings — solar variability, volcanic eruptions (whose erupted particles and gases block sunlight), aerosols (tiny particles suspended in the air) from pollution, and greenhouse gases (CO₂ is the main one). Solar variability and volcanic eruptions are obviously natural climate forcings, while aerosols and greenhouse gases are anthropogenic, meaning they are related to human activities. The history of these forcings is shown in the figure below.

   

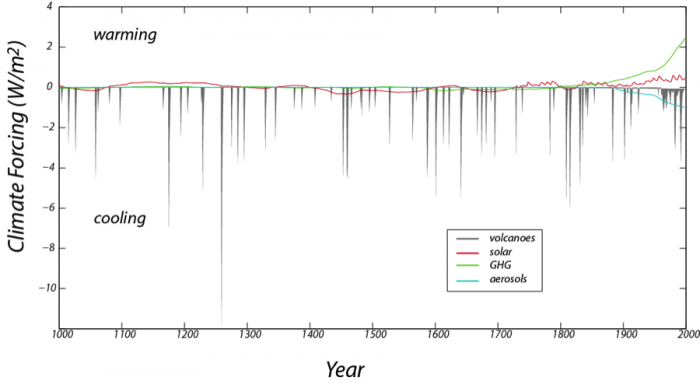   The reconstructed record of important climate forcings over the past 1000 years (data from Crowley, 2000). Positive values lead to warming, while negative values lead to cooling. Note that although volcanoes have very strong cooling effects, these effects are very short-lived.

   Credit: David Bice © Penn State University is licensed under CC BY-NC-SA 4.0

   Volcanoes, by spewing ash and sulfate gases into the atmosphere block sunlight and thus have a cooling effect. This history is based on the human records of eruptions in recent times and ash deposits preserved in ice cores (which we can date because they have annual layers — we count backward from the present) and sediment cores for older times. Note that although the volcanoes have a strong cooling effect, the history consists of very brief events. The solar variability comes from actual measurements in recent times and further back in time, on the abundance of an isotope of Beryllium, whose production in the atmosphere is a function of solar intensity — this isotope falls to the ground and is preserved in ice cores. The greenhouse gas forcing record is based on actual measurements in recent times and ice core records further in the past (the ice contains tiny bubbles that trap samples of the atmosphere from the time the snow fell). The aerosol record is based entirely on historical observations and is 0 earlier in times before we began to burn wood and coal on a large scale.

   In this experiment, we will add the history of these forcings over the last 1000 years and see how our climate system responds, comparing the model temperature with the best estimates for what the temperature actually was over that time period. Solar variability, volcanic eruptions, and aerosols all change the E_in or Insolation part of the model, while the greenhouse gas forcing change the E_out part of the model. We can turn the forcings on and off by flicking some switches, and thus get a clear sense of what each of them does and which of them is the most important at various points in time.

   We can compare the model temperature history with the reconstructed (also referred to in the model as “observed”) temperature history for this time period, which comes from a combination of thermometer measurements in recent times and temperature proxy data for the earlier part of the history (these are data from tree rings, corals, stalactites, and ice cores, all of which provide an indirect measure of temperature). This observed temperature record, shown in graph #1 on the model, is often referred to as the “hockey stick” because it resembles (to some) a hockey stick with the upward-pointing blade on the right side of the graph.

   First, open the model with the forcings built-in, and study the Model Diagram to get a sense of how the forcings are applied to the model. If you run the model with all of the switches in the off position, you will see our familiar steady state model temperature of 15°C over the whole length of time. The model time goes from the year 1000 to 1998 because the forcings are from a paper published in 2000.

   Graph #1 plots the model temperature and the observed temperature in °C, graph #2 plots the 4 forcings in terms of W/m², graph #5 plots the cumulative temperature difference between the model and the observed temperature (it takes the absolute value of the temperature difference at each time step and then adds them up — the lower this number at the end of time, the closer the match between the model and the observed temperatures), and graph #6 shows the same thing, but it begins keeping track of these differences in 1850, so it focuses on the more recent part of the history. Graph #1 gives you a visual comparison of the model and the observed temperatures, while graphs #5 and 6 give you a more quantitative sense of how the model compares with reality.

   Video: A Simple Climate Model with 1000 years of Forcings (Questions 6-7) (3:33)

   Click here for a transcript of the Simple Climate Model with 1000 years of Forcings (Questions 6-7).

   The model that you're going to use for problems six and seven is this one here. It's the same climate model that we've worked at before, in essence, but here we're running it for a much longer time, from the year 1000 up until 1998. And over that time, we're applying to the model, the best estimates of four different climate forcings, things that can change the climate. One is greenhouse gas concentrations, another is aerosols, these are fine particulates, essentially pollution in the atmosphere. Then there are volcanic forcings, so whenever there is an eruption, all the particles thrown up into the atmosphere tend to block sunlight and cause cooling. And then there's a solar variability, that's another forcing, and that changes over the course of time as the Sun gets brighter or dimmer. So, each of these forcings has a switch associated with it. You can turn them. They’re in the on position now. You can turn them off here, and we'll just run the model really quickly here, and you'll see two things on this graph. One is in red, the model temperature, so our climate model temperature, about 15 degrees steady through time. And then, in blue, is the observed temperature. This is the reconstructed temperature over this time period based on all sorts of studies of different climate proxies. And so, the idea is that if we have a relatively good climate model and we apply these four principal forcings to it, we should be able to kind of closely match this observed temperature curve here in blue. So, we can turn these things on and see what they do. There's the greenhouse gas concentration, here's the aerosol concentration combined with greenhouse gases. And I'm going to combine the volcanic forcing, and finally, the solar forcing. So, we see all four kinds of principal climate forcings added in here. One variable here is the ocean depth, the depth of the ocean water that's involved in relatively short-term climate change. Watch what happens if I increase that. I’ll just increase it to four hundred and something. I'll run it again and watch what happens to these abrupt little cooling spikes that are associated with volcanic eruptions. You see they get diminished greatly if the ocean depth is greater, and that's just because these volcanic eruptions are such short-lived forcings, that if the ocean that's involved in climate is very deep, it doesn't change much, it doesn't have time to change much, because these volcanic events are so short. So, that really dampens the cooling effect there and you get a much closer match to the curve here. So, in these questions, you'll be asked to try out various combinations of these forcings and evaluate the match between the model temperature and the observed temperature here, and there are two questions to answer with respect to this model.

   Credit: Dutton

6. Before running the model set the ocean depth to 50 m. Run the model 4 times with each of the forcing switches turned on separately (i.e., only one forcing switch turned on for each model run) and evaluate which of the forcings does the best job of matching the shape of the observed temperature curve from 1800 to 1998. Which one provides the best match?

   A. GHG

   B. Aerosols

   C. Volcanoes

   D. Solar

7. Before running the model, set the ocean depth to 150 m. Run the model 3 times — once with only the natural forcing switches turned, once with only the anthropogenic forcings turned on, and once with all of them turned on. Which combination does the best job of matching the shape of the observed temperature curve from 1800 to 1998?

   A. natural forcings

   B. anthropogenic forcings

   C. all forcings

   D. natural and anthropogenic forcings are about the same.